Fortsetzbarkeit der Lösungen

Fortsetzbarkeit der Lösungen

Neben der Differentialgleichung (17.1), die wir autonom nennen, treten auch Differentialgleichungen auf, deren rechte Seite explizit von der Zeit abhängt und die deshalb nichtautonom heißen:

(17.11)

Dabei sei

mit

eine

-Abbildung. Durch die neue Variable

läßt sich (17.11) als autonome Differentialgleichung

interpretieren. Die Lösung von (17.11) mit Anfang

zur Zeit

wird mit

bezeichnet.

Um die globale Existenz der Lösungen und damit die Existenz eines Flusses von (17.1) zu zeigen, sind folgende Sätze oft hilfreich.
1. Kriterium von Wintner und Conti: Ist in (17.1) und existiert eine stetige Funktion , so daß für alle gilt und ist 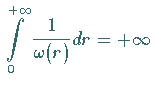, so läßt sich jede Lösung von (17.1) auf ganz fortsetzen.

Beispiel

Für das Kriterium von WINTNER und CONTI sind folgende Funktionen geeignet: und , wobei eine Konstante ist.

2. Fortsetzungsprinzip: Bleibt eine Lösung von (17.1) für wachsende Zeiten beschränkt, so existiert sie für alle positiven Zeiten und damit auf ganz .
Voraussetzung: Im weiteren wird stets die Existenz eines Flusses von (17.1) vorausgesetzt.

Beispiel
	Für das Kriterium von WINTNER und CONTI sind folgende Funktionen geeignet: und , wobei eine Konstante ist.