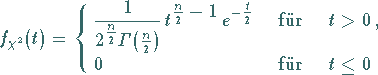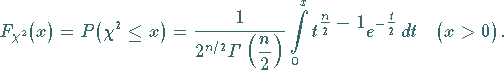Chi-Quadrat-Verteilung
1. Dichte und Verteilungsfunktion:
Es seien 
unabhängige,
(
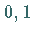)-normalverteilte Zufallsveränderliche.
Dann heißt die Verteilung der Zufallsveränderlichen
 |
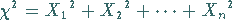(16.89) |
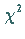-Verteilung mit dem Freiheitsgrad 
.
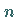Ihre Verteilungsfunktion wird mit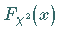 
bezeichnet, die zugehörige
Dichtefunktion mi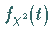t 
.
Es gilt:
 |
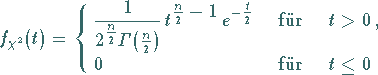(16.90a) |
 |
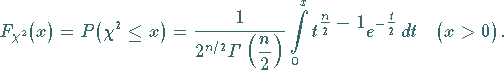(16.90b) |
2. Erwartungswert und Streuung:
 |
(16.91) |
3.
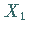Sind 
und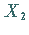 
unabhängige Zufallsveränderliche, die je einer
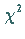-Verteilung mit 
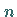bzw.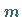 
Freiheitsgraden genügen, so ist die
Zufallsveränderliche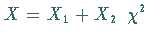 
-verteilt mit 
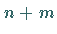Freiheitsgraden.
4. Dichtefunktionen bei verschiedenen Zufallsveränderlichen
:
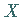Sind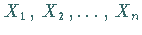 
unabhängige, (
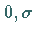)-normalverteilte
Zufallsveränderliche, so besitzt
5. Quantile:
Für die Quantile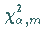 
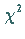der -Verteilung mit
dem Freiheitsgrad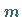
(s. Abbildung) gilt
 |
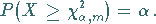(16.95) |
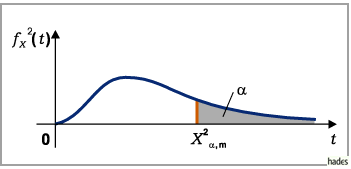
Quantile der 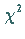-Verteilung sind in der zugehörigen
Tabelle Chi-Quadrat-Verteilung zu
finden.
