Weibull-Verteilung
1. Verteilungsfunktion und Dichte:
Die stetige Zufallsgröße 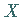 genügt einer WEIBULL-Verteilung mit den
Parametern
genügt einer WEIBULL-Verteilung mit den
Parametern 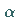 und
und 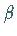 (
(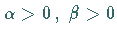 ), wenn ihre Dichte durch
), wenn ihre Dichte durch
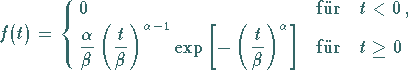 |
(16.84) |
und ihre Verteilungsfunktion durch
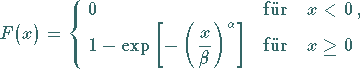 |
(16.85) |
gegeben sind.
2. Erwartungswert und Streuung:
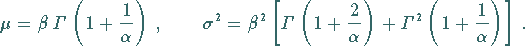 |
(16.86) |
Mit 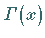 wird dabei die Gammafunktion bezeichnet:
wird dabei die Gammafunktion bezeichnet:
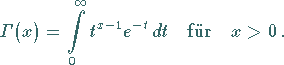 |
(16.87) |
In (16.84) ist 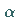 der Form- und
der Form- und 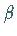 der Maßstabsparameter
(s. die folgenden zwei Abbildungen):
der Maßstabsparameter
(s. die folgenden zwei Abbildungen):
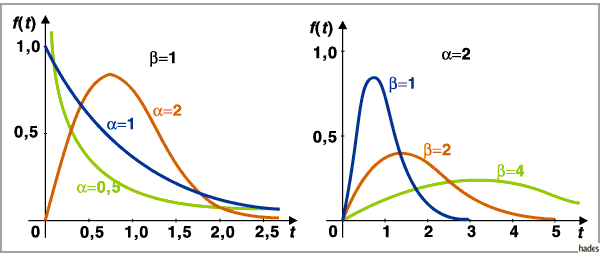
Bemerkungen
a) Für 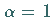 geht die WEIBULL-Verteilung in die
Exponentialverteilung mit dem Parameter
geht die WEIBULL-Verteilung in die
Exponentialverteilung mit dem Parameter 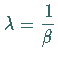 über.
über.
b) Die WEIBULL-Verteilung gibt es auch als dreiparametrige Verteilung,
wenn zusätzlich der Parameter 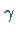 als sogenannter Lageparameter eingeführt wird.
Die Verteilungsfunktion lautet dann:
als sogenannter Lageparameter eingeführt wird.
Die Verteilungsfunktion lautet dann:
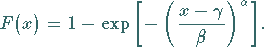 |
(16.88) |
c) Die WEIBULL-Verteilung wird besonders in der
Zuverlässigkeitstheorie angewendet, weil sie in sehr flexibler Weise die Funktionsdauer
von Bauteilen oder Baugruppen beschreiben kann.
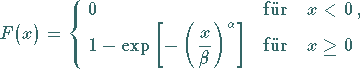
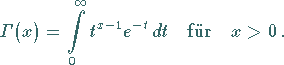
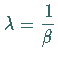 über.
über.