Flächeninterpretation der Wahrscheinlichkeit, Quantil
Durch die Einführung der Verteilungsfunktion und der Wahrscheinlickeitsdichte in
(16.43) und (16.45) kann die Wahrscheinlichkeit
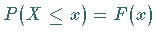 als Flächeninhalt interpretiert werden, und zwar als Inhalt der
Fläche zwischen Dichtefunktion
als Flächeninhalt interpretiert werden, und zwar als Inhalt der
Fläche zwischen Dichtefunktion 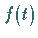 und der Abszisse im Intervall
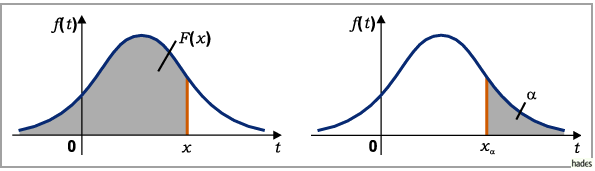
und der Abszisse im Intervall 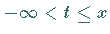 (s. linke Abbildung).
(s. linke Abbildung).
Häufig wird eine Wahrscheinlichkeit 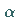 vorgegeben.
Gilt
vorgegeben.
Gilt
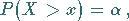 |
(16.47) |
dann nennt man die zugehörige Abszisse 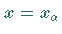 Quantil oder auch
Fraktil der Verteilung (s. rechte Abbildung).
Quantil oder auch
Fraktil der Verteilung (s. rechte Abbildung).
Das bedeutet: Der Flächeninhalt unter der Dichtefunktion 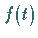 rechts von
rechts von 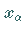 ist gleich
ist gleich 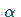 .
.
Hinweis: In der Literatur wird allerdings auch die Fläche links von 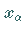 zur Definition des Quantils verwendet.
zur Definition des Quantils verwendet.
In der mathematischen Statistik wird für kleine Werte 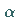 (z.B.
(z.B. 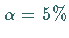 oder
oder 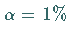 )
manchmal der Begriff Irrtumswahrscheinlichkeit verwendet.
Die dazugehörigen Quantile sind für die wichtigsten praktischen Verteilungen
tabelliert worden (s. Tabelle POISSON-Verteilung bis Tabelle
STUDENT-Verteilung).
)
manchmal der Begriff Irrtumswahrscheinlichkeit verwendet.
Die dazugehörigen Quantile sind für die wichtigsten praktischen Verteilungen
tabelliert worden (s. Tabelle POISSON-Verteilung bis Tabelle
STUDENT-Verteilung).
![]() zur Definition des Quantils verwendet.
zur Definition des Quantils verwendet.
![]() (z.B.
(z.B. ![]() oder
oder ![]() )
manchmal der Begriff Irrtumswahrscheinlichkeit verwendet.
Die dazugehörigen Quantile sind für die wichtigsten praktischen Verteilungen
tabelliert worden (s. Tabelle POISSON-Verteilung bis Tabelle
STUDENT-Verteilung).
)
manchmal der Begriff Irrtumswahrscheinlichkeit verwendet.
Die dazugehörigen Quantile sind für die wichtigsten praktischen Verteilungen
tabelliert worden (s. Tabelle POISSON-Verteilung bis Tabelle
STUDENT-Verteilung).