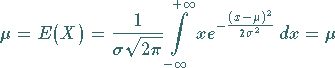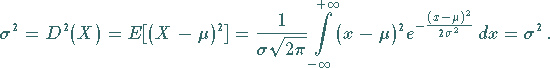Normalverteilung
1. Verteilungsfunktion und Dichte:
Eine Zufallsveränderliche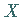 
mit der Verteilungsfunktion
 |
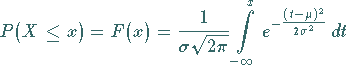(16.69) |
heißt normalverteilt , genauer
(
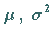)- normalverteilt .
Die Funktion
 |
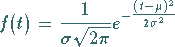(16.70) |
heißt die Dichte der Normalverteilung.
Sie nimmt an der Stelle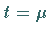 
ihr Maximum an und hat Wendepunkte
bei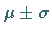 
(s. Abbildung):
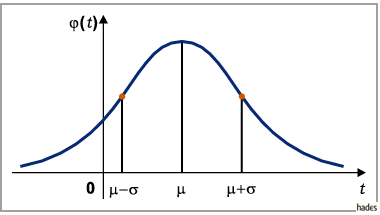
2. Erwartungswert und Streuung:
Erwartungswert und Streuung ergeben sich für die Parameter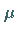 
und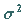 
der
Normalverteilung zu
 |
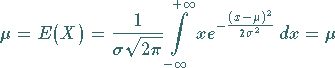(16.71a) |
und
 |
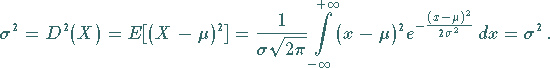(16.71b) |
Sind die Zufallsveränderlichen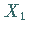 
und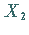 
unabhängig und normalverteilt mit den
Parametern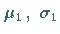 
bzw.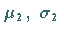 
,
so ist auch die
Zufallsveränderliche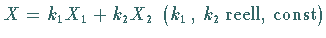 
normalverteilt mit den Parametern
.
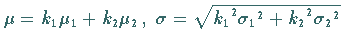Die Berechnung der Wahrscheinlichkeit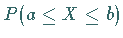 
erfolgt mit Hilfe der normierten
Normalverteilung 
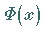gemäß
 |
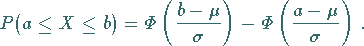(16.72) |
