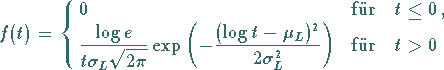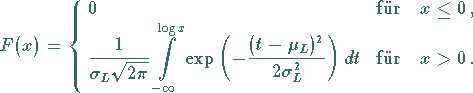Logarithmische Normalverteilung
Dichte, Verteilungsfunktion, Erwartungswert und Streuung
1. Verteilungsfunktion und Dichte:
Die stetige Zufallsgröße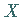 
,
die alle positiven Werte annehmen kann, besitzt
eine logarithmische Normalverteilung (auch Lognormalverteilung genannt) mit
den Parametern 
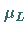und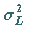 
,
wenn die Zufallsgröße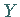 
mit
 |
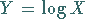(16.76) |
normalverteilt ist mit den Parametern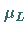
und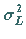 
.
Die Zufallsgröße
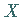hat demzufolge die Dichte
 |
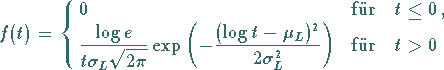(16.77) |
und die Verteilungsfunktion
 |
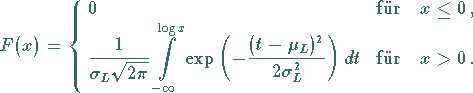(16.78) |
Bei praktischen Anwendungen wird als Logarithmus entweder der natürliche oder der
dekadische Logarithmus verwendet.
2. Erwartungswert und Streuung:
Für Erwartungswert und Streuung der Lognormalverteilung erhält man, wenn der
natürliche Logarithmus verwendet wird:
 |
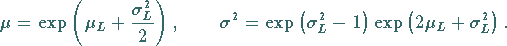(16.79) |
Bemerkungen:
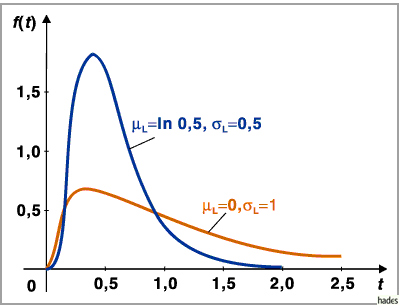
a) Die Dichtefunktion der Lognormalverteilung ist links durch Null begrenzt
und läuft rechts flach aus.
Die folgende Abbildung zeigt die Dichte der Lognormalverteilung für verschiedene Werte
von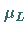
und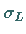 
.
Dabei wurde der natürliche Logarithmus verwendet.
b) Man beachte: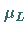
und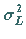
sind Erwartungswert und Streuung
der transformierten Zufallsgröße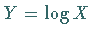 
,
währe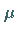nd 
und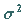 
gemäß (16.79) Erwartungswert und Streuung der
Zufallsgröße X sind.
c) Die Verteilungsfunktion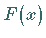 
der Lognormalverteilung kann mit Hilfe der
Verteilungsfunktion 
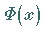der normierten Normalverteilung
berechnet werden, denn es gilt:
 |
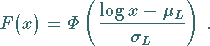(16.80) |
d) Die Lognormalverteilung wird häufig bei Lebensdaueranalysen von
ökonomischen, technischen und biologischen Vorgängen angewendet.
e) Während die Normalverteilung mit der additiven Überlagerung einer
großen Anzahl voneinander unabhängiger zufälliger Ereignisse in Zusammenhang
gebracht werden kann, ist es bei der Lognormalverteilung das multiplikative Zusammenwirken
vieler zufälliger Einflüsse.
