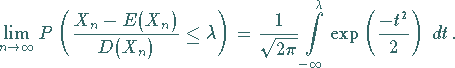Binomialverteilung
Sind bei einem Versuch nur die beiden Ereignisse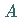 
und 
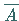möglich und
sind die dazuzugehörigen Wahrscheinlichkeiten
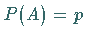und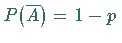 
,
so ist
 |
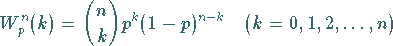(16.61) |
die Wahrscheinlichkeit dafür, daß bei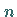 
-maliger Wiederholung des Versuches das
Ereignis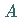
genau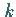 
-mal eintritt.
Bei jedem Ziehen eines unabhängigen Elements aus der Grundgesamtheit gilt
 |
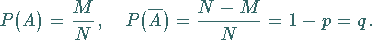(16.62) |
Die Wahrscheinlichkeit, bei den ersten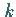
Ziehungen ein Element mit der Eigenschaft
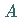zu ziehen und bei den darauffolgenden 
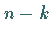ein Element mit der Eigenschaft
,
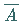ist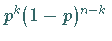 
.
Dabei ist die Reihenfolge der Ziehung der Elemente ohne Bedeutung, da die Kombinationen
 |
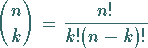(16.63) |
die gleiche Wahrscheinlichkeit haben und auch zu einer Stichprobe mit dem Umfang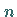
mit
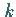Elementen der Eigenschaft
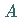führen.
Eine Zufallsveränderliche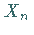 
,
bei der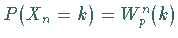 
ist, heißt
binomialverteilt mit den Parametern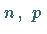 
.
Es gilt:
1. Erwartungswert und Streuung:
 |
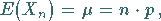(16.64a) |
 |
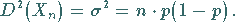(16.64b) |
2. Ist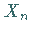 
binomialverteilt, so ist
 |
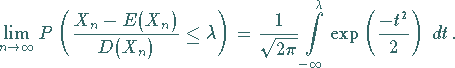(16.64c) |
Demnach läßt sich die Binomialverteilung für große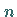
näherungsweise durch
eine Normalverteilung mit den Parametern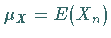 
und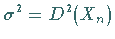 
ersetzen.
Dies ist mit im allgemeinen ausreichender Genauigkeit möglich, wenn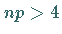 
und
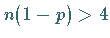ist.
3. Rekursionsformel:
Für praktische Rechnungen ist die folgende Rekursionsformel der Binomialverteilung
nützlich:
 |
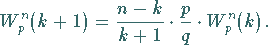(16.64d) |
4. Si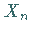nd
und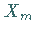 
mit den Parametern 
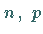bzw.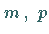 
binomialverteilte Zufallsveränderliche, so ist die Zufallsveränderliche
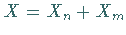ebenfalls binomialverteilt, und zwar mit den Parametern
.
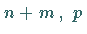In der folgenden Abbildung sind drei Binomialverteilungen für die Fälle
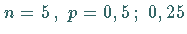und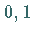 
dargestellt.
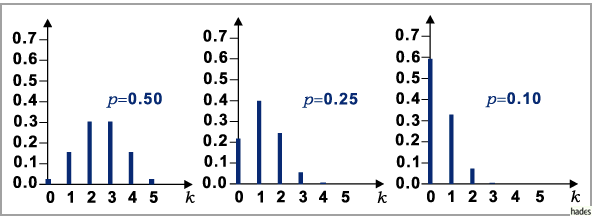
Die Abbildung zeigt auch, daß sich in Übereinstimmung mit der Symmetrie der
Binomialkoeffizienten für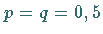 
eine Symmetrie der Binomialverteilung ergibt.
Mit der Entfernung des Wertes 
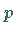von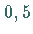 
nimmt diese Symmetrie ab.
