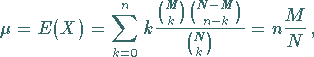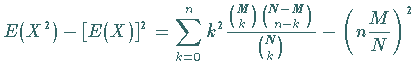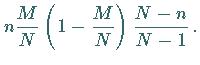Hypergeometrische Verteilung
Wie bei der Betrachtung der Binomialverteilung liege eine zweistufige Grundgesamtheit mit
zwei Klassen von Elementen vor, von denen die eine Klasse 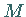 Elemente mit der Eigenschaft
Elemente mit der Eigenschaft
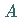 enthält, die andere
enthält, die andere 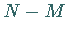 Elemente, die die Eigenschaft
Elemente, die die Eigenschaft 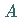 nicht besitzen.
Im Unterschied zu dem auf die Binomialverteilung führenden Fall mit Zurücklegen der
gezogenen Kugeln des Urnenmodells wird jetzt der Fall ohne Zurücklegen betrachtet.
nicht besitzen.
Im Unterschied zu dem auf die Binomialverteilung führenden Fall mit Zurücklegen der
gezogenen Kugeln des Urnenmodells wird jetzt der Fall ohne Zurücklegen betrachtet.
Die Wahrscheinlichkeit dafür, daß sich unter 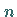 gezogenen Kugeln
gezogenen Kugeln 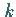 schwarze
befinden, ist durch
schwarze
befinden, ist durch
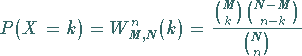 |
(16.65a) |
mit
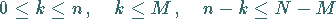 |
(16.65b) |
gegeben.
Die Wahrscheinlichkeiten 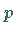 und
und 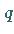 berechnet man gemäß (16.61).
berechnet man gemäß (16.61).
Eine Zufallsgröße 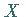 ,
die der Verteilung (16.65a) genügt, heißt
hypergeometrisch verteilt.
,
die der Verteilung (16.65a) genügt, heißt
hypergeometrisch verteilt.
1. Erwartungswert und Streuung:
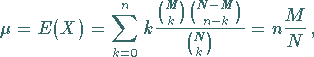 |
(16.66a) |
2. Rekursionsformel:
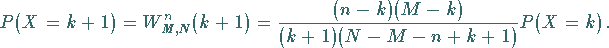 |
(16.66c) |
In der folgenden Abbildung sind drei hypergeometrische Verteilungen für die Fälle
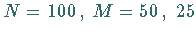 und
und 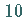 für
für  dargestellt, was den Fällen
dargestellt, was den Fällen
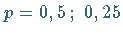 und
und 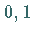 der sich anschließenden Abbidung zur
Binomialverteilung entspricht.
der sich anschließenden Abbidung zur
Binomialverteilung entspricht.
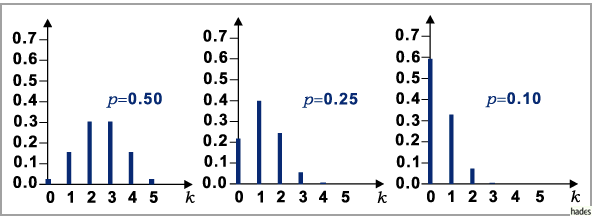
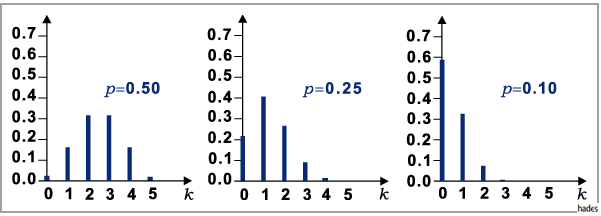
In diesen Beispielen sind keine signifikanten Unterschiede zwischen Binomial- und
hypergeometrischer Verteilung zu erkennen.
![]() ,
die der Verteilung (16.65a) genügt, heißt
hypergeometrisch verteilt.
,
die der Verteilung (16.65a) genügt, heißt
hypergeometrisch verteilt.