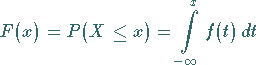1. Diskrete Zufallsgröße:
Eine diskrete Zufallsveränderliche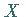 
,
die die Werte 
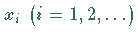mit den Wahrscheinlichkeiten 
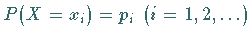annimmt, hat
die Verteilungsfunktion
 |
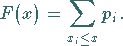(16.44) |
2. Kontinuierliche Zufallsgröße:
Bei einer kontinuierlichen Zufallsgröße ist die Wahrscheinlichkeit dafür, daß
sie einen bestimmten Wert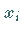 
annimmt, gleich 
.
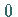Man betrachtet daher die Wahrscheinlichkeit dafür, daß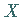 
in einem endlichen
Intervall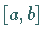 
liegt.
Läßt sich diese mit Hilfe einer Funktion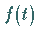 
,
der
Wahrscheinlichkeitsdichte , in der Form
 |
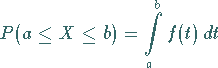(16.45) |
darstellen, dann spricht man von einer stetigen Verteilungsfunktion
 |
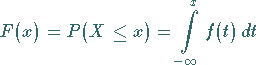(16.46) |
und einer stetigen Zufallsgröße .
Hinweis: Wenn keine Verwechslung mit der oberen Integrationsgrenze möglich ist,
wird häufig die Integrationsveränderliche anstelle von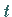 
mit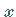 
bezeichnet.
