1. Zur Bestimmung der Regressionskoeffizienten hätte man auch von der
Interpolationsbedingung
,
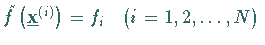d.h.
von
 |
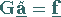(16.168) |
ausgehen können.
Im Falle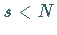 
stellt (16.168) ein überbestimmtes lineares
Gleichungssystem dar, zu dessen genäherter Lösung das
HOUSEHOLDER-Verfahren verwendet werden kann.
Der Übergang von (16.168), d.h. Multiplikation von
(16.168) mit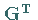 
,
wird auch als
GAUSS-Transformation bezeichnet.
Wenn die Spalten der Matrix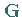 
linear unabhängig sind, also Rang
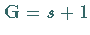ist, dann hat das Normalgleichungssystem (16.164e)
eine eindeutige Lösung, die mit der nach HOUSEHOLDER ermittelten
Näherungslösung von (16.168) übereinstimmt.
2. Auch im mehrdimensionalen Fall lassen sich mit Hilfe der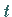 
-Verteilung
Vertrauensgrenzen für die Regressionskoeffizienten analog zu (16.160a,b)
angeben (s. Lit. 16.11).
3. Mit Hilfe der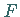 
-Verteilung kann man einen sogenannten Adäquatheitstest
für den Ansatz (16.164b) durchführen.
Dieser Test gibt Auskunft darüber, ob ein Ansatz der Form (16.164b), aber mit
weniger Gliedern, schon eine hinreichend gute Approximation der theoretischen
Regressionsfunktion (16.161) liefert (s. Lit. 16.11).
