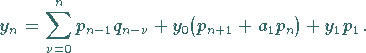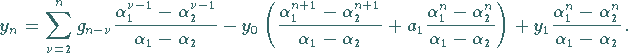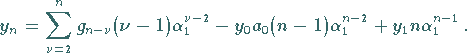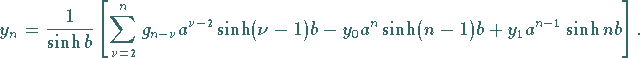Differenzengleichung 2. Ordnung (Anfangswertaufgabe)
Die Differenzengleichung 2. Ordnung lautet:
 |
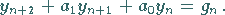(15.136) |
Als Anfangswerte sind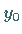 
und 
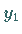gegeben.
Mit Hilfe des zweiten Verschiebungssatzes erhält man zu
(15.136) die Bildgleichung
 |
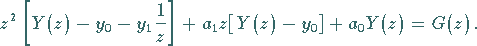(15.137) |
Setzt man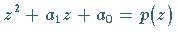 
,
dann lautet die Bildfunktion
 |
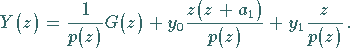(15.138) |
Das Polynom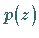 
habe die Nullstellen 
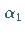und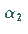 
,
für die
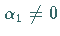und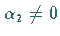 
gelte, weil sonst 
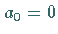wäre und
sich die Differenzengleichung auf eine solche erster Ordnung reduzieren würde.
Durch Partialbruchzerlegung und Anwendung der Tabelle Z-Transformationen
ergibt sich aus
Wegen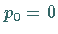 
ist nach dem zweitem Verschiebungssatz
 |
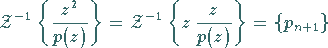(15.139b) |
und nach dem ersten Verschiebungssatz
 |
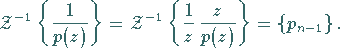(15.139c) |
Dabei ist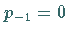 
zu setzen.
Mit Hilfe des Faltungssatzes erhält man die Originalfolge mit
 |
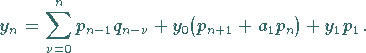(15.139d) |
Wegen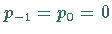 
ergibt sich daraus mit (15.139a)
 |
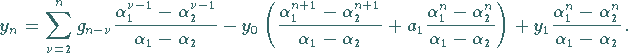(15.139e) |
Diese Form läßt sich noch wegen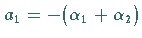 
und
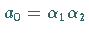(s. Wurzelsatz von VIETA)
noch zu
 |
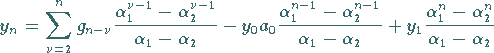(15.139f) |
vereinfachen.
Für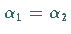 
erhält man analog
 |
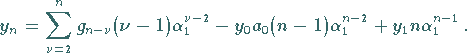(15.139g) |
Bei der Differenzengleichung 2. Ordnung läßt sich die Rücktransformation
der Bildfunktion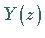 
auch ohne Partialbruchzerlegung durchführen, wenn man
Korrespondenzen wie z.B.
 |
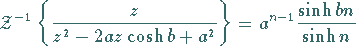(15.140a) |
benutzt und auch hier den zweiten Verschiebungssatz anwendet.
Mit der Substitution
lautet die Originalfolge zu
(15.138):
 |
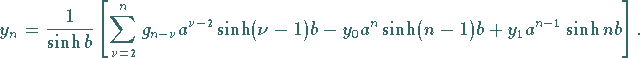(15.140b) |
Diese Formel ist günstig für eine numerische Auswertung besonders dann, wenn 
und 
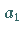komplexe Zahlen sind.
Die hyperbolischen Funktionen sind auch für komplexe Argumente definiert.
