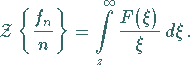Rechenregeln
Für die Anwendung der Z-Transformation ist es wichtig zu wissen, wie sich gewisse
Operationen an den Originalfolgen in entsprechenden Operationen an den Bildfunktionen
widerspiegeln und umgekehrt.
Im folgenden sei 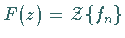 für
für 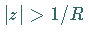 .
.
1. Translation
Man unterscheidet eine Vorwärts- und eine Rückwärtsverschiebung.
a) Erster Verschiebungssatz:
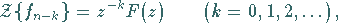 |
(15.117) |
dabei wird 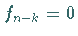 für
für 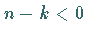 festgelegt.
festgelegt.
b) Zweiter Verschiebungssatz:
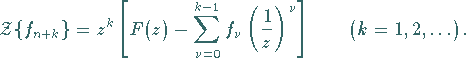 |
(15.118) |
2. Summation
Für 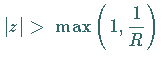 gilt:
gilt:
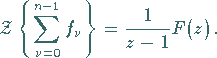 |
(15.119) |
3. Differenzenbildung
Für die Differenzen
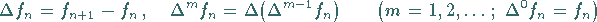 |
(15.120) |
gilt die Regel:
4. Dämpfung
Für 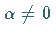 ,
beliebig komplex,
,
beliebig komplex, 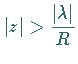 gilt:
gilt:
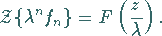 |
(15.122) |
5. Faltung
Als Faltung zweier Folgen 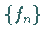 und
und 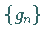 bezeichnet man die Operation
bezeichnet man die Operation
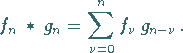 |
(15.123) |
Existieren die Z-Transformierten 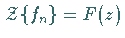 für
für 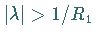 und
und 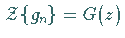 für
für 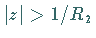 ,
dann gilt
,
dann gilt
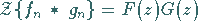 |
(15.124) |
für 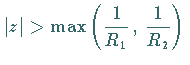 .
Die Beziehung (15.124) wird auch als Faltungssatz
der Z-Transformation bezeichnet.
Er entspricht der Vorschrift für die Multiplikation zweier Potenzreihen.
.
Die Beziehung (15.124) wird auch als Faltungssatz
der Z-Transformation bezeichnet.
Er entspricht der Vorschrift für die Multiplikation zweier Potenzreihen.
6. Differentiation der Bildfunktion
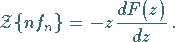 |
(15.125) |
Durch wiederholte Anwendung von (15.125) lassen sich auch Ableitungen
höherer Ordnung von 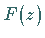 bestimmen.
bestimmen.
7. Integration der Bildfunktion
Unter der Voraussetzung 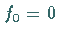 gilt
gilt
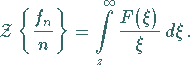 |
(15.126) |
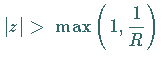 gilt:
gilt:
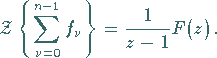
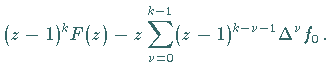
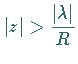 gilt:
gilt:
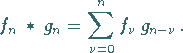
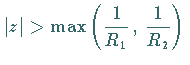 .
Die Beziehung (15.124) wird auch als Faltungssatz
der Z-Transformation bezeichnet.
Er entspricht der Vorschrift für die Multiplikation zweier Potenzreihen.
.
Die Beziehung (15.124) wird auch als Faltungssatz
der Z-Transformation bezeichnet.
Er entspricht der Vorschrift für die Multiplikation zweier Potenzreihen.