Allgemeine Lösung linearer Differenzengleichungen

Allgemeine Lösung linearer Differenzengleichungen

Eine lineare Differenzengleichung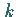

-ter Ordnung mit konstanten Koeffizienten hat die Form

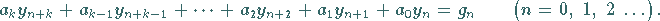(15.133)

Dabei ist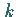

eine natürliche Zahl. Die Koeffizienten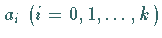

sind gegebene reelle oder komplexe Zahlen und hängen nicht von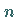

ab. Es gelte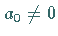

und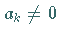

. Die Folge

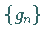ist gegeben, die Folge

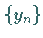ist gesucht.

Zur Festlegung einer bestimmten Lösung von (15.133) werden die Werte 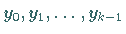vorgegeben. Dann kann man aus (15.133) für den nächsten Wert 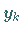ausrechnen. Aus 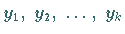ergibt sich dann aus (15.133) für der Wert 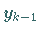. Auf diese Weise kann man alle Werte 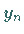rekursiv ausrechnen. Mit Hilfe der Z-Transformation läßt sich jedoch für 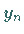eine allgemeine Darstellung angeben. Dazu wendet man den zweiten Verschiebungssatz (15.118) auf (15.133) an und erhält:


			(15.134)

Dabei bedeutet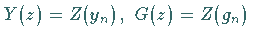

. Setzt man weiterhin

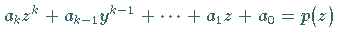, so lautet die Lösung der sogenannten Bildgleichung (15.134)

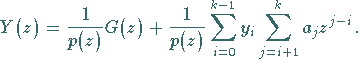(15.135)

Wie bei der Behandlung von linearen Differentialgleichungen mit der LAPLACE-Transformation hat man auch bei der Z-Transformation den Vorteil, daß die Anfangswerte in die Bildgleichung eingehen und daher bei der Lösung automatisch berücksichtigt werden. Aus (15.135) gewinnt man dann die gesuchte Lösung

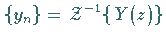durch Rücktransformation gemäß Abschnitt
Umkehrung der Z-Transformation.