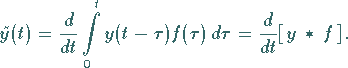Die charakteristische Gleichung 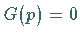 dieser Differentialgleichung habe nur einfache
Wurzeln
dieser Differentialgleichung habe nur einfache
Wurzeln 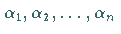 ,
von denen keine gleich Null ist.
Für die Störfunktion
,
von denen keine gleich Null ist.
Für die Störfunktion 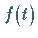 können zwei Fälle betrachtet werden.
können zwei Fälle betrachtet werden.
1. Ist die Störfunktion 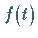 gleich der in der Praxis häufig auftretenden
Sprungfunktion
gleich der in der Praxis häufig auftretenden
Sprungfunktion 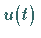 ,
dann lautet die Lösung:
,
dann lautet die Lösung:
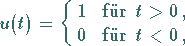 |
(15.54a) |
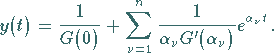 |
(15.54b) |
2. Für eine allgemeine Störfunktion 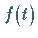 erhält man die Lösung
erhält man die Lösung
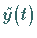 aus (15.54b) in Gestalt der DUHAMELschen
Formel, die die Faltung benutzt:
aus (15.54b) in Gestalt der DUHAMELschen
Formel, die die Faltung benutzt:
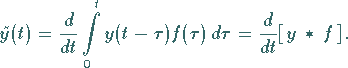 |
(15.55) |