Faltung
1. Faltung im Originalbereich
Als Faltung zweier Funktionen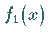 
und 
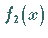bezeichnet man das Integral
 |
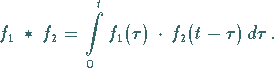(15.21) |
Die Gleichung (15.21) wird auch einseitige Faltung im
Intervall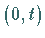 
genannt.
Eine zweiseitige Faltung tritt bei der FOURIER-Transformation
(Faltung im Intervall (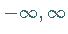
)) auf.
Die Faltung (15.21) besitzt die Eigenschaften
 |
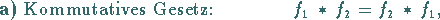(15.22a) |
 |
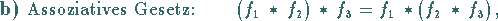(15.22b) |
 |
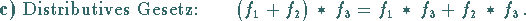(15.22c) |
Im Bildbereich entspricht der Faltung die gewöhnliche Multiplikation:
 |
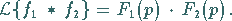(15.23) |
In der folgenden Abbildung ist die Faltung zweier Funktionen graphisch dargestellt.
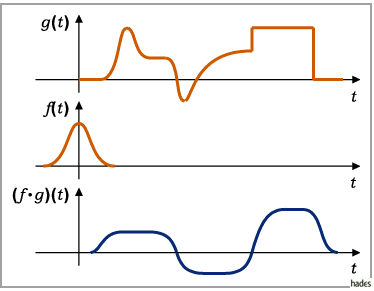
Man kann den Faltungssatz zur Bestimmung der Originalfunktion wie folgt benutzen:
1. Faktorisierung der Bildfunktion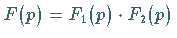 
.
2. Ermittlung der Originalfunktionen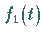 
und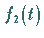 
der Bildfunktionen
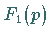und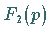 
gemäß Tabelle.
3. Bildung der Originalfunktion durch Faltung von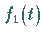
mit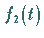
im
Originalbereich gemäß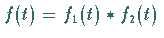 
,
die zur gegebenen Bildfunktion
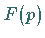gehört.
2. Faltung im Bildbereich (komplexe Faltung)
 |
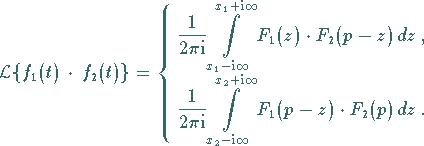(15.24) |
Die Integration erfolgt längs einer Parallelen zur imaginären Achse.
Im ersten Integral müssen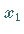 
und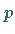 
so gewählt werden, daß 
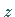in der
Konvergenzhalbebene von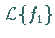 
liegt und 
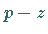in der
Konvergenzhalbebene von 
.
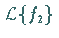Entsprechendes gilt für das zweite
Integral.
