Ist 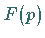 ist eine meromorphe Funktion , die sich als Quotient zweier ganzer, also
in überall konvergente Potenzreihen entwickelbare Funktionen ohne gemeinsame Nullstellen
darstellen läßt, und die daher in eine Summe aus einer ganzen Funktion und unendlich
vielen Partialbrüchen zerlegbar ist, dann gilt der Zusammenhang
ist eine meromorphe Funktion , die sich als Quotient zweier ganzer, also
in überall konvergente Potenzreihen entwickelbare Funktionen ohne gemeinsame Nullstellen
darstellen läßt, und die daher in eine Summe aus einer ganzen Funktion und unendlich
vielen Partialbrüchen zerlegbar ist, dann gilt der Zusammenhang
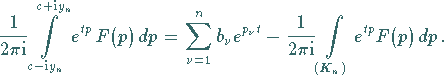 |
(15.44) |
Dabei sind die 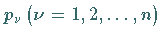 Pole 1. Ordnung der Funktion
Pole 1. Ordnung der Funktion 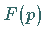 ,
die
,
die 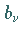 die zugehörigen Residuen, die
die zugehörigen Residuen, die 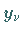 gewisse Ordinaten
und
gewisse Ordinaten
und 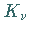 gewisse Kurvenzüge, etwa Halbkreise in der in der folgenden Abbildung
angedeuteten Art.
gewisse Kurvenzüge, etwa Halbkreise in der in der folgenden Abbildung
angedeuteten Art.
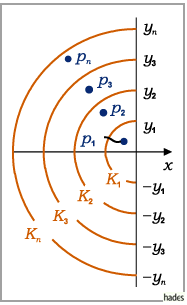
Die Lösung 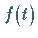 erhält man in der Form
erhält man in der Form
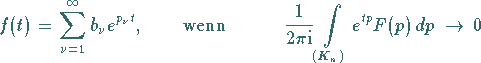 |
(15.45) |
für 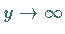 strebt, was allerdings nicht immer leicht nachzuweisen ist.
In manchen Fällen, wenn z.B. der rationale Anteil der meromorphen Funktion
strebt, was allerdings nicht immer leicht nachzuweisen ist.
In manchen Fällen, wenn z.B. der rationale Anteil der meromorphen Funktion 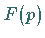 identisch Null ist, bedeutet das eben gewonnene Ergebnis eine formale Übertragung des
HEAVYSIDEschen Entwicklungssatzes auf meromorphe Funktionen.
identisch Null ist, bedeutet das eben gewonnene Ergebnis eine formale Übertragung des
HEAVYSIDEschen Entwicklungssatzes auf meromorphe Funktionen.
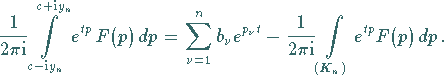
![]() Pole 1. Ordnung der Funktion
Pole 1. Ordnung der Funktion ![]() ,
die
,
die ![]() die zugehörigen Residuen, die
die zugehörigen Residuen, die ![]() gewisse Ordinaten
und
gewisse Ordinaten
und ![]() gewisse Kurvenzüge, etwa Halbkreise in der in der folgenden Abbildung
angedeuteten Art.
gewisse Kurvenzüge, etwa Halbkreise in der in der folgenden Abbildung
angedeuteten Art.
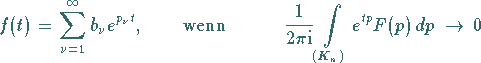
![]() strebt, was allerdings nicht immer leicht nachzuweisen ist.
In manchen Fällen, wenn z.B. der rationale Anteil der meromorphen Funktion
strebt, was allerdings nicht immer leicht nachzuweisen ist.
In manchen Fällen, wenn z.B. der rationale Anteil der meromorphen Funktion ![]() identisch Null ist, bedeutet das eben gewonnene Ergebnis eine formale Übertragung des
HEAVYSIDEschen Entwicklungssatzes auf meromorphe Funktionen.
identisch Null ist, bedeutet das eben gewonnene Ergebnis eine formale Übertragung des
HEAVYSIDEschen Entwicklungssatzes auf meromorphe Funktionen.