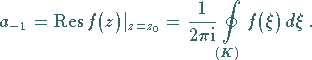|
|
|
|
der Potenz 
in der
LAURENT-Entwicklung von 
bezeichnet man als
Residuum der Funktion
im singulären Punkt 
:
 |
(14.54a) |
Das zu einem Pol 
-ter Ordnung gehörende Residuum kann mit der Formel
Wenn die Funktion als Quotient gemäß 
dargestellt
werden kann, wobei die Funktionen 
und 
im Punkt 
analytisch und
eine einfache Wurzel der Gleichung 
sein soll, so
daß 
ist, dann ist der Punkt 
ein Pol 1. Ordnung der Funktion 
.
Mit (14.54b) ergibt sich:
 |
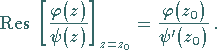(14.54c) |
Wenn
eine -fache Wurzel der Gleichung
ist, d.h., wenn
ist, dann ist der Punkt
ein -facher Pol der Funktion .
|
|
