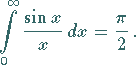Integralsinus
Integralsinus nennt man das Integral
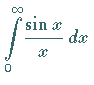 .
Untersucht wird in Analogie zum vorangegangenen Beispiel
das komplexe Integral
.
Untersucht wird in Analogie zum vorangegangenen Beispiel
das komplexe Integral 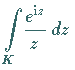 ,
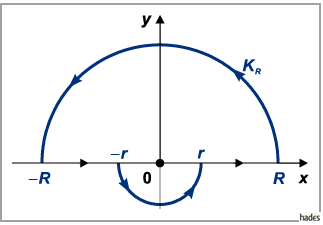
mit der Kurve
,
mit der Kurve
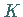 gemäß der folgenden Abbildung.
gemäß der folgenden Abbildung.
Der Integrand des komplexen Integrals hat an der Stelle  einen Pol 1. Ordnung, so
daß
einen Pol 1. Ordnung, so
daß
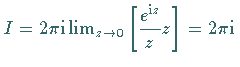 ,
also
,
also
 .
.
Führt man die Grenzübergänge 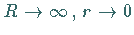 durch,
wobei der Integrand des zweiten Integrals für
durch,
wobei der Integrand des zweiten Integrals für 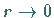 bezüglich
bezüglich 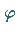 gleichmäßig gegen 1 konvergiert (d.h., der Grenzübergang
gleichmäßig gegen 1 konvergiert (d.h., der Grenzübergang 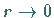 kann
unter dem Integralzeichen vollzogen werden), dann erhält man unter Beachtung des
Lemma von JORDAN
kann
unter dem Integralzeichen vollzogen werden), dann erhält man unter Beachtung des
Lemma von JORDAN
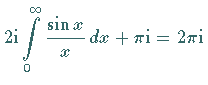 ,
also
,
also
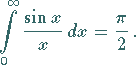 |
(14.59) |
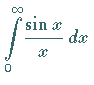 .
Untersucht wird in Analogie zum vorangegangenen Beispiel
das komplexe Integral
.
Untersucht wird in Analogie zum vorangegangenen Beispiel
das komplexe Integral 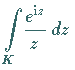 ,
mit der Kurve
,
mit der Kurve
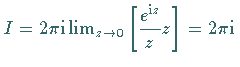 ,
also
,
also
 .
.
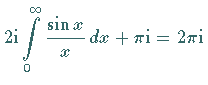 ,
also
,
also