Dem gesuchten reellen Integral
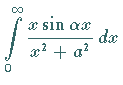 wird auf folgende Weise ein komplexes Integral zugeordnet:
wird auf folgende Weise ein komplexes Integral zugeordnet:
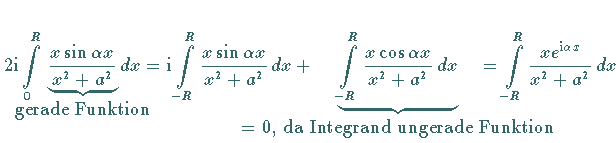 .
.
Das letzte dieser Integrale ist Bestandteil des komplexen Integrals
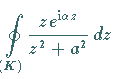 .
Die Kurve
.
Die Kurve 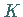 besteht aus dem oben definierten Halbkreisbogen
besteht aus dem oben definierten Halbkreisbogen 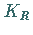 und dem Stück der
reellen Achse zwischen
und dem Stück der
reellen Achse zwischen 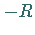 und
und 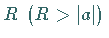 .
Der komplexe Integrand hat in der oberen Halbebene nur die singuläre Stelle
.
Der komplexe Integrand hat in der oberen Halbebene nur die singuläre Stelle
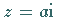 .
Nach dem Residuensatz gilt:
.
Nach dem Residuensatz gilt:
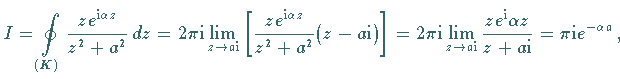 so daß
so daß
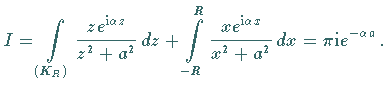
Aus 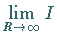 ergibt sich unter Beachtung des
Lemmas von JORDAN:
ergibt sich unter Beachtung des
Lemmas von JORDAN:
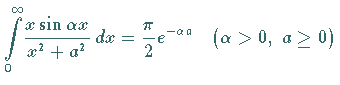 .
.
Auf ähnliche Weise wurden weitere Integrale der Tabelle
Bestimmte Integrale berechnet.
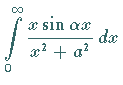 wird auf folgende Weise ein komplexes Integral zugeordnet:
wird auf folgende Weise ein komplexes Integral zugeordnet:
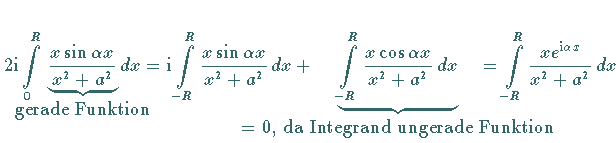 .
.
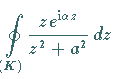 .
Die Kurve
.
Die Kurve 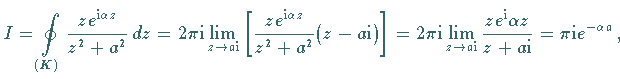 so daß
so daß
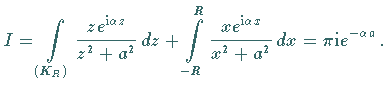
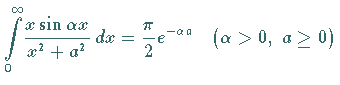 .
.