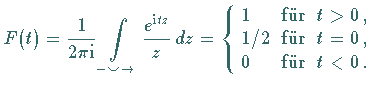Unstetige reelle Funktionen kann man mit Hilfe komplexer Integrale, sogenannter
Hakenintegrale nach der Form des Integrationsweges darstellen.
Die folgende spezielle Sprungfunktion ist ein Beispiel.
 |
|
|
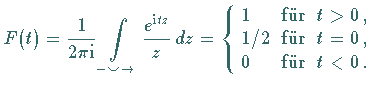(14.60) |
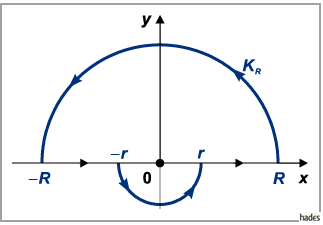
Das Symbol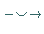 
bezeichnet einen Integrationsweg längs
der reellen Achse 
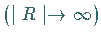unter Umgehung des Nullpunktes
(s. Abbildung).
Deutet man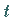 
als Zeit, dann stellt die Funktion 
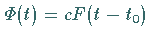eine
Größe dar, die zur Zeit 
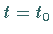von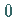 
über den Wert 
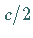auf den Wert 
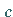springt.
Die Sprungfunktion wird in der Elektrotechnik zur Darstellung plötzlich auftretender
Strom- oder Spannungsstöße verwendet (s. auch Sprungfunktion).
