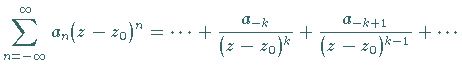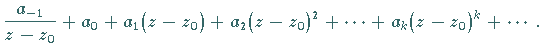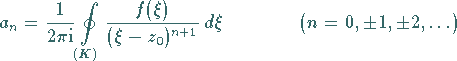|
Für die Funktion 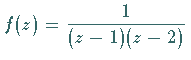 ,
die im Ringgebiet ,
die im Ringgebiet 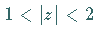 analytisch ist, soll eine LAURENT-Reihenentwicklung bezüglich
analytisch ist, soll eine LAURENT-Reihenentwicklung bezüglich 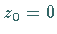 angegeben
werden.
Dazu kann man die Funktion
angegeben
werden.
Dazu kann man die Funktion 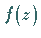 durch Partialbruchzerlegung auf die Form
durch Partialbruchzerlegung auf die Form
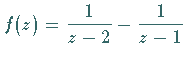 bringen.
Durch einfache Umformung können diese beiden Terme als geometrische Reihen dargestellt
werden, die gemeinsam in dem Ringgebiet
bringen.
Durch einfache Umformung können diese beiden Terme als geometrische Reihen dargestellt
werden, die gemeinsam in dem Ringgebiet 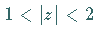 konvergieren.
Man erhält:
konvergieren.
Man erhält:
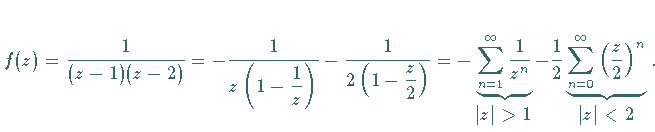
|