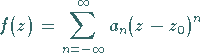|
|
|
|
in der Umgebung eines Punktes 
analytisch ist, nicht aber
in
selbst, dann heißt
eine isolierte singuläre Stelle der Funktion
.
Ist
in der Umgebung von
in die LAURENT-Reihe
 |
(14.51) |
entwickelbar, dann können die isolierten singulären Stellen nach dem Verhalten der
LAURENT-Reihen eingeteilt werden:
1. Enthält die LAURENT-Reihe keine Glieder mit negativen Potenzen von
,
wobei 
für 
gilt, dann geht die
LAURENT-Entwicklung in die TAYLOR-Reihe mit den aus der
CAUCHYschen Integralformel folgenden Koeffizienten
 |
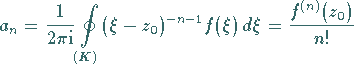(14.52) |
ist dann auch im Punkt
analytisch, wenn 
ist oder wenn
eine hebbare Singularität ist.
,
wobei gelten soll 
,
alle
für 
,
dann spricht man von einer außerwesentlichen Singularität im Punkt
oder
einem Pol der Ordnung 
oder Pol der Vielfachheit ;
durch Multiplikation
mit 
,
aber keiner niedrigeren Potenz, geht
in eine Funktion über,
die in
und Umgebung analytisch ist.
| Beispiel | |
|
| |
3. Enthält die LAURENT-Reihe unendlich viele Glieder mit negativen
Potenzen von ,
dann ist
ein wesentlich singulärer Punkt
der Funktion .
Bei Annäherung an einen Pol wächst 
über alle Grenzen.
Bei Annäherung an eine wesentlich singuläre Stelle kommt
jeder beliebigen
komplexen Zahl 
beliebig nahe.
| Beispiel | |
|
Die Funktion | |
|
|
hat an der Stelle 
einen Pol
1. Ordnung.
,
deren LAURENT-Reihe
lautet, hat an der
Stelle