Taylor-Reihe
Jede im Innern eines Gebietes 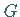 analytische Funktion
analytische Funktion 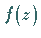 kann für jeden Punkt
kann für jeden Punkt
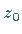 in
in 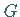 eindeutig in eine Potenzreihe der Form
eindeutig in eine Potenzreihe der Form
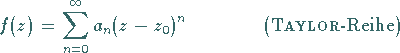 |
(14.48a) |
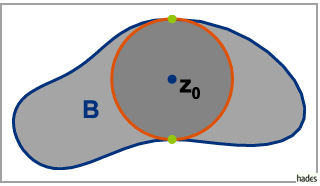
entwickelt werden, wobei der Konvergenzkreis der größte Kreis um 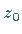 ist, der
noch ganz dem Gebiet
ist, der
noch ganz dem Gebiet  angehört (s. Abbildung).
angehört (s. Abbildung).
Für die im allgemeinen komplexen Koeffizienten 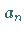 der Potenzreihe gilt
der Potenzreihe gilt
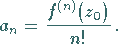 |
(14.48b) |
Die TAYLOR-Reihe kann daher in der Form
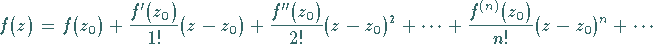 |
(14.48c) |
geschrieben werden.
Innerhalb ihres Konvergenzkreises ist jede Potenzreihe die TAYLOR-Entwicklung
ihrer Summenfunktion.
Beispiele für TAYLOR-Entwicklungen sind die Reihendarstellungen der Funktionen
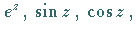
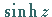 und
und  in
Unterkapitel Elementare transzendente Funktionen.
in
Unterkapitel Elementare transzendente Funktionen.
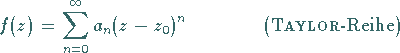
![]() ist, der
noch ganz dem Gebiet
ist, der
noch ganz dem Gebiet ![]() angehört (s. Abbildung).
angehört (s. Abbildung).
![]()
![]() und
und ![]() in
Unterkapitel Elementare transzendente Funktionen.
in
Unterkapitel Elementare transzendente Funktionen.