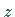|
|
|
|
nur Pole als singuläre
Stellen, dann heißt sie meromorph .
Eine meromorphe Funktion läßt sich immer als Quotient analytischer Funktionen
darstellen.
Beispiele für in der ganzen Ebene meromorphe Funktionen sind die rationalen Funktionen,
die nur eine endliche Zahl von Polen besitzen, sowie solche transzendenten Funktionen
wie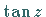 
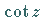und 
.
|
|