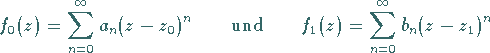|
Die geometrischen Reihen 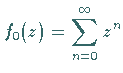 mit dem Konvergenzkreis
mit dem Konvergenzkreis
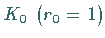 um
um 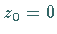 und
und
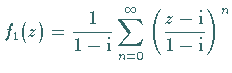 mit dem Konvergenzkreis
mit dem Konvergenzkreis 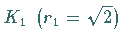 um
um 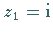 haben jede in
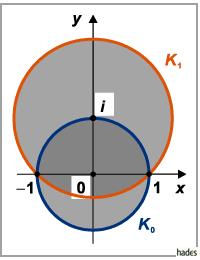
ihrem Konvergenzkreis und in dem gemeisamen (in der Abbildung doppelt schraffierten)
Konvergenzgebiet dieselbe für
haben jede in
ihrem Konvergenzkreis und in dem gemeisamen (in der Abbildung doppelt schraffierten)
Konvergenzgebiet dieselbe für 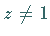 analytische Funktion
analytische Funktion 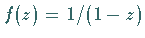 als
Summe.
Daher ist
als
Summe.
Daher ist 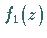 analytische Fortsetzung von
analytische Fortsetzung von 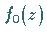 aus
aus 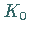 in
in 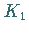 hinein (und
umgekehrt).
hinein (und
umgekehrt).
|