Grenzwert der komplexen Funktion
Grenzwert einer Funktion 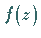 heißt eine komplexe Zahl
heißt eine komplexe Zahl 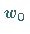 ,
wenn
für
,
wenn
für 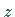 gegen
gegen 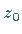 die Funktion
die Funktion 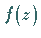 gegen
gegen 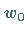 strebt:
strebt:
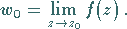 |
(14.1a) |
Dazu ist erforderlich, daß sich eine beliebig kleine positive Zahl 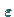 angeben läßt, für die es eine reelle positive Zahl
angeben läßt, für die es eine reelle positive Zahl 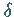 derart gibt, daß
für jede beliebige komplexe Zahl
derart gibt, daß
für jede beliebige komplexe Zahl 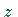 ,
ausgenommen höchstens die Zahl
,
ausgenommen höchstens die Zahl 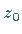 selbst,
die Ungleichungen
selbst,
die Ungleichungen
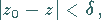 |
(14.1b) |
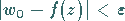 |
(14.1c) |
erfüllt sind.
Die geometrische Bedeutung geht aus der folgenden Abbildung hervor:
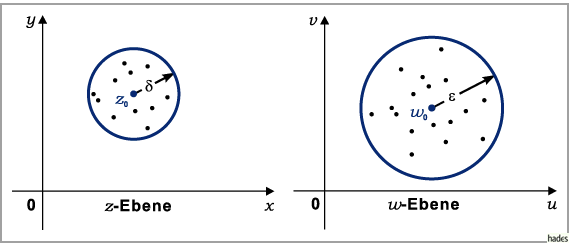
Einem beliebigen Punkt 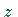 ,
ausgenommen höchstens den Punkt
,
ausgenommen höchstens den Punkt 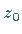 selbst, der
innerhalb eines Kreises mit dem Mittelpunkt
selbst, der
innerhalb eines Kreises mit dem Mittelpunkt 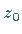 und dem Radius
und dem Radius 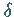 liegt,
entspricht in der
liegt,
entspricht in der 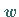 -Ebene, in die die Funktion
-Ebene, in die die Funktion 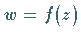 abbildet, ein Punkt
abbildet, ein Punkt 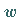 ,
der in einem Kreis mit dem Mittelpunkt
,
der in einem Kreis mit dem Mittelpunkt 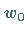 und dem Radius
und dem Radius 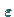 liegt.
Die Flächen mit den beliebig kleinen Radien nennt man auch die beliebig kleinen
Umgebungen
liegt.
Die Flächen mit den beliebig kleinen Radien nennt man auch die beliebig kleinen
Umgebungen 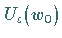 und
und 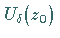 .
.