Gebrochenlineare Funktion
Für die konforme Abbildung in der Form der gebrochenlinearen Funktion
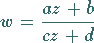 |
(14.13a) |
kann die Transformation in drei Schritte zerlegt werden:
 |
(14.13b) |
 |
(14.13c) |
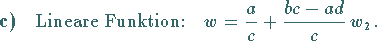 |
(14.13d) |
Es werden wieder Kreise in Kreise überführt ( Kreisverwandtschaft ), wobei
Geraden als Kreise mit 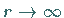 aufgefaßt werden.
Fixpunkte dieser konformen Abbildung sind die beiden Punkte, die der quadratischen
Gleichung
aufgefaßt werden.
Fixpunkte dieser konformen Abbildung sind die beiden Punkte, die der quadratischen
Gleichung 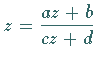 genügen.
Sind die Punkte
genügen.
Sind die Punkte 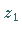 und
und 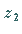 Spiegelpunkte in bezug auf den Kreis
Spiegelpunkte in bezug auf den Kreis 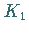 der
der 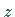 -Ebene,
dann sind ihre Bildpunkte
-Ebene,
dann sind ihre Bildpunkte 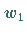 und
und 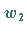 in der
in der 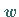 -Ebene ebenfalls Spiegelpunkte in
bezug auf den Bildkreis
-Ebene ebenfalls Spiegelpunkte in
bezug auf den Bildkreis 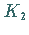 von
von 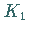 .
Das orthogonale Netz, das in das orthogonale kartesische Netz der
.
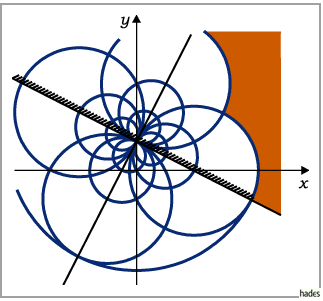
Das orthogonale Netz, das in das orthogonale kartesische Netz der 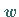 -Ebene übergeht,
ist in der folgenden Abbildung dargestellt.
-Ebene übergeht,
ist in der folgenden Abbildung dargestellt.
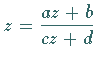 genügen.
Sind die Punkte
genügen.
Sind die Punkte