Inversion
Bei der Inversion genannten konformen Abbildung
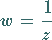 |
(14.12) |
geht ein Punkt 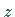 der
der 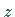 -Ebene mit dem Radius
-Ebene mit dem Radius 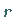 und dem Argument
und dem Argument 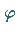 in einen Punkt
in einen Punkt 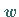 der
der 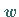 -Ebene mit dem Radius
-Ebene mit dem Radius 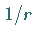 und dem Argument
und dem Argument 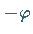 über.
Die orthogonalen Netze der Transformation zeigt die Abbildung.
über.
Die orthogonalen Netze der Transformation zeigt die Abbildung.
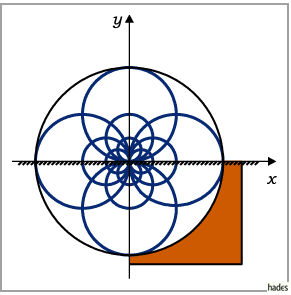
Die Transformation von (14.12)beschreibt eine Spiegelung an einem Kreis mit
dem Radius 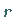 und eine Spiegelung an der reellen Achse (s. die folgende Abbildung).
und eine Spiegelung an der reellen Achse (s. die folgende Abbildung).
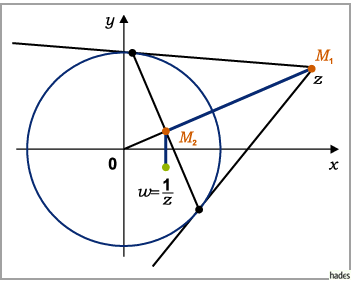
Bei der Inversion geht ein Punkt 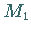 mit dem Radius
mit dem Radius 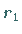 innerhalb des Kreises mit
dem Radius
innerhalb des Kreises mit
dem Radius 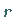 in einen Punkt
in einen Punkt 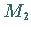 über, der auf der Verlängerung des gleichen
Radiusvektors
über, der auf der Verlängerung des gleichen
Radiusvektors 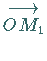 außerhalb des Kreises liegt
und den Abstand
außerhalb des Kreises liegt
und den Abstand 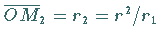 vom Mittelpunkt
vom Mittelpunkt  hat.
hat.
Der Einheitskreis der 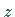 -Ebene geht in den Einheitskreis der
-Ebene geht in den Einheitskreis der 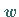 -Ebene wegen
-Ebene wegen
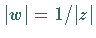 über (s. Abbildung).
über (s. Abbildung).
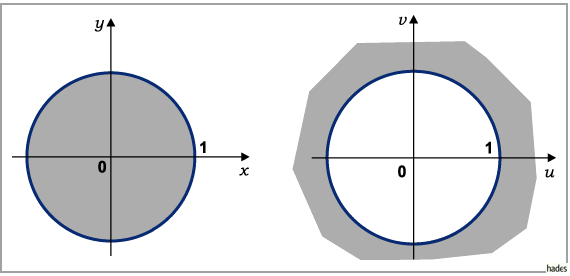
Allgemein gehen Kreise in Kreise über, wobei Geraden als Grenzfälle mit
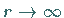 zu den Kreisen gerechnet werden.
Punkte, die im Innern des Kreises liegen, werden zu äußeren Punkten und umgekehrt.
Der Punkt
zu den Kreisen gerechnet werden.
Punkte, die im Innern des Kreises liegen, werden zu äußeren Punkten und umgekehrt.
Der Punkt  geht in
geht in 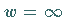 über, d.h., die Konformität ist hier gestört.
Die Fixpunkte der konformen Abbildung sind
über, d.h., die Konformität ist hier gestört.
Die Fixpunkte der konformen Abbildung sind 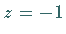 und
und  .
.