Nullstellen, Beschränktheit, Maximalwert
1. Nullstellen:
Da der Absolutbetrag einer Funktion positiv ist, liegt das Relief stets oberhalb der
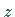-Ebene, ausgenommen alle Punkte, in denen 
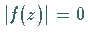gilt, also 
.
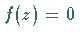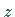Man nennt -Werte, für die 
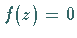ist, die Nullstellen der Funktion
.
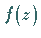2. Beschränktheit:
Eine Funktion heißt in einem gegebenen Gebiet beschränkt , wenn die
Bedingung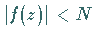 
erfüllt werden kann, wobei 
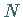eine konstante positive Zahl
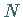ist.
Im entgegengesetzten Falle, wenn es keine derartige Zahl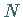
gibt, heißt die Funktion
nicht beschränkt.
3. Satz über den Maximalwert:
Wenn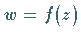 
in einem abgeschlossenen Gebiet eine analytische Funktion ist, dann liegt
das Maximum ihres Betrages auf dem Rande.
4. Satz über die Konstanz oder Satz von Liouville:
Wenn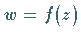
in der gesamten Ebene analytisch und beschränkt ist, dann ist diese
Funktion eine Konstante: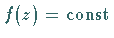 
.
