Ableitung einer Vektorfunktion
Die Ableitung der Vektorfunktion einer skalaren Variablen von
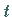 (13.1) nach
(13.1) nach 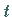 ist eine neue Vektorfunktion von
ist eine neue Vektorfunktion von 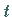 :
:
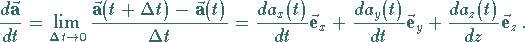 |
(13.2) |
Die Ableitung 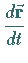 des Radiusvektors stellt geometrisch betrachtet
einen Vektor dar, der in die Richtung der Tangente des Hodographen im Punkt
des Radiusvektors stellt geometrisch betrachtet
einen Vektor dar, der in die Richtung der Tangente des Hodographen im Punkt 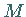 weist
(s. Abbildung).
weist
(s. Abbildung).
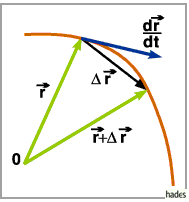
Seine Länge hängt von der Wahl des Parameters 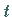 ab.
Wenn
ab.
Wenn 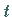 die Zeit ist, dann beschreibt
die Zeit ist, dann beschreibt 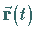 die Bewegung des Punktes
die Bewegung des Punktes 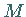 im
Raum, während
im
Raum, während 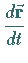 Größe und Richtung der Geschwindigkeit
dieser Bewegung angibt.
Ist
Größe und Richtung der Geschwindigkeit
dieser Bewegung angibt.
Ist  die Bogenlänge der Raumkurve, gemessen von einem bestimmten Kurvenpunkt an,
dann gilt
die Bogenlänge der Raumkurve, gemessen von einem bestimmten Kurvenpunkt an,
dann gilt 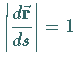 .
.
![]() des Radiusvektors stellt geometrisch betrachtet
einen Vektor dar, der in die Richtung der Tangente des Hodographen im Punkt
des Radiusvektors stellt geometrisch betrachtet
einen Vektor dar, der in die Richtung der Tangente des Hodographen im Punkt ![]() weist
(s. Abbildung).
weist
(s. Abbildung).
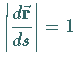 .
.