Vektorfunktion, Hodograph
1. Vektorfunktion einer skalaren Variablen
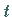wird ein Vektor 
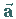genannt, wenn seine Komponenten Funktionen von
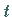sind:
 |
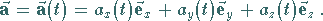(13.1) |
Die Begriffe Grenzwert, Stetigkeit und Differenzierbarkeit lassen sich von
den Komponenten des Vektors 
auf den Vektor selbst übertragen.
2. Hodograph einer Vektorfunktion
Faßt man die Vektorfunktion
als Orts- oder Radiusvektor
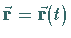eines Punktes 
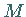auf, dann beschreibt dieser bei
Änderung von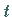
eine Raumkurve (s. Abbildung).
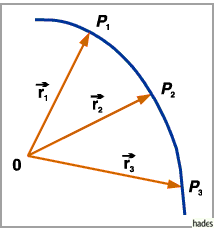
Man bezeichnet diese Raumkurve auch als Hodograph der Vektorfunktion 
.
