Koordinatendarstellung von Skalarfeldern
Wenn die Punkte eines Raumteiles durch ihre Koordinaten gegeben werden, z.B. durch
kartesische, Zylinder- oder Kugelkoordinaten, dann erhält man zur Beschreibung des
zugehörigen skalaren Feldes (13.6a) im allgemeinen eine
Funktion dreier Veränderlicher:
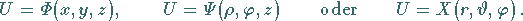 |
(13.8a) |
Im Falle eines ebenen Feldes genügt eine Funktion zweier Veränderlicher.
Für kartesische oder Polarkoordinaten hat sie die Form:
 |
(13.8b) |
Es wird vorausgesetzt, daß die Funktionen in (13.8a) und (13.8b)
im allgemeinen stetig sind, ausgenommen einige Unstetigkeitspunkte, -kurven oder
-flächen.
Die Funktionen lauten
a) für ein Zentralfeld:
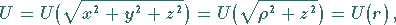 |
(13.9a) |
b) für ein Axialfeld:
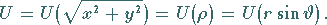 |
(13.9b) |
Die Untersuchung von zentralen Feldern führt man am besten unter Zuhilfenahme von
Kugelkoordinaten durch, von axialen Feldern mit Hilfe von Zylinderkoordinaten.