Vergleich mit der linearen Algebra, Residualspektrum

Vergleich mit der linearen Algebra, Residualspektrum

Ein wesentlicher Unterschied zwischen dem endlichdimensionalen Fall, der im wesentlichen in der linearen Algebra betrachtet wird, und der Situation im unendlichdimensionalen Fall, mit dem sich die Funktionalanalysis befaßt, besteht zumindest an dieser Stelle darin, daß in ersterem stets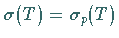

gilt, während in letzterem das Spektrum in der Regel Punkte enthält, die keine Eigenwerte von

sind. Ist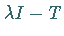

injektiv und surjektiv, dann gilt wegen des Satzes über die Stetigkeit des Inversen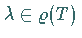

. Im Kontrast zum endlichdimensionalen Fall, bei dem die Surjektivität automatisch aus der Injektivität folgt, muß im unendlichdimensionalen Falle weitaus differenzierter vorgegangen werden.

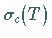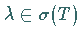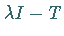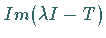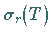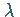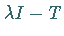Die Menge aller , für die injektiv und dicht in liegt, heißt stetiges oder kontinuierliches Spektrum und die Menge aller der , mit injektivem und nichtdichtem Wertebereich, heißt Rest- oder Residualspektrum des Operators .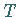

Für einen beschränkten linearen Operator im komplexen BANACH-Raum gilt die disjunkte Vereinigung

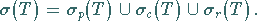(12.156)