Satz von Banach über die Stetigkeit des inversen Operators
Satz: Ist  ein linearer stetiger bijektiver Operator von
ein linearer stetiger bijektiver Operator von  auf
auf 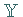 ,
dann
ist der inverse Operator
,
dann
ist der inverse Operator 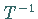 stetig.
stetig.
Anwendungen: Als wichtige Anwendungen ergeben sich daraus beispielsweise die
Stetigkeit von 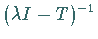 bei Injektivität und Surjektivität von
bei Injektivität und Surjektivität von
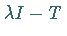 ,
was bei der Untersuchung des
Spektrums eines Operators von Bedeutung ist, sowie die
,
was bei der Untersuchung des
Spektrums eines Operators von Bedeutung ist, sowie die
Stetige Abhängigkeit der Lösung sowohl von der rechten Seite als auch von den
Anfangswerten bei Anfangswertproblemen für lineare Differentialgleichungen .
Das soll an der folgenden Anfangswertaufgabe gezeigt werden:
| Beispiel |
|
Das Anfangswertproblem
|
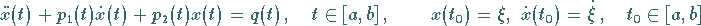 |
(12.144a) |
mit den Koeffizienten 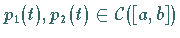 besitzt für jede rechte
Seite
besitzt für jede rechte
Seite 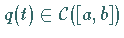 und jedes Zahlenpaar
und jedes Zahlenpaar 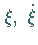 genau eine
Lösung
genau eine
Lösung 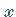 aus
aus 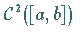 ,
die im folgenden Sinne stetig von
,
die im folgenden Sinne stetig von
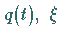 und
und 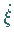 abhängt.
Sind
abhängt.
Sind 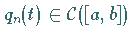 und gilt für
und gilt für 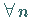
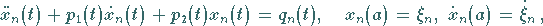 |
(12.144b) |
dann gilt:
 |
(12.144c) |
