Die Methode der sukzessiven Approximation eignet sich zur Lösung
einer Gleichung der Form
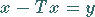 |
(12.145) |
mit einem stetigen linearen Operator  im BANACH-Raum
im BANACH-Raum  bei vorgegebenem
bei vorgegebenem
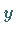 .
Sie besteht darin, ausgehend von einer beliebigen Anfangsnäherung
.
Sie besteht darin, ausgehend von einer beliebigen Anfangsnäherung 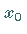 ,
eine Folge
,
eine Folge
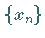 von Näherungslösungen nach der Vorschrift
von Näherungslösungen nach der Vorschrift
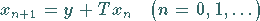 |
(12.146) |
zu erzeugen, die in  zur Lösung
zur Lösung 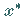 von (12.145) konvergiert.
Die Konvergenz der Methode, also
von (12.145) konvergiert.
Die Konvergenz der Methode, also 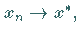 basiert auf der Konvergenz
der Reihe (12.140) mit
basiert auf der Konvergenz
der Reihe (12.140) mit  .
.
Sei 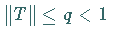 ,
dann gelten die folgenden Aussagen:
,
dann gelten die folgenden Aussagen:
a) Der Operator 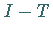 besitzt einen stetigen Inversen mit
besitzt einen stetigen Inversen mit
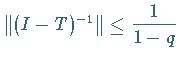 ,
und die Gleichung
(12.145) hat genau
eine Lösung für beliebiges
,
und die Gleichung
(12.145) hat genau
eine Lösung für beliebiges 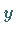 .
.
b) Die Reihe (12.140) konvergiert, und ihre Summe ist der
Operator 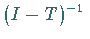 .
.
c) Das Verfahren (12.146) konvergiert für einen
beliebigen Anfangswert 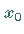 zur eindeutigen Lösung
zur eindeutigen Lösung 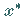 der Gleichung
(12.145), falls die Reihe (12.140) konvergiert.
Dabei gilt die Abschätzung
der Gleichung
(12.145), falls die Reihe (12.140) konvergiert.
Dabei gilt die Abschätzung
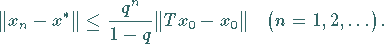 |
(12.147) |
Analog (s. Lineare Integralgleichungen und
Lit. 12.9) behandelt man Gleichungen der Typen
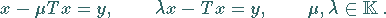 |
(12.148) |
![]() ,
dann gelten die folgenden Aussagen:
,
dann gelten die folgenden Aussagen:
![]() besitzt einen stetigen Inversen mit
besitzt einen stetigen Inversen mit
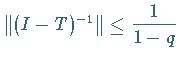 ,
und die Gleichung
(12.145) hat genau
eine Lösung für beliebiges
,
und die Gleichung
(12.145) hat genau
eine Lösung für beliebiges ![]() .
.
![]() .
.
![]() zur eindeutigen Lösung
zur eindeutigen Lösung ![]() der Gleichung
(12.145), falls die Reihe (12.140) konvergiert.
Dabei gilt die Abschätzung
der Gleichung
(12.145), falls die Reihe (12.140) konvergiert.
Dabei gilt die Abschätzung