Inverser Operator
Seien  und
und 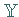 beliebige normierte Räume und
beliebige normierte Räume und
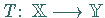 ein linearer, nicht unbedingt stetiger
Operator.
Dann besitzt
ein linearer, nicht unbedingt stetiger
Operator.
Dann besitzt  einen stetigen Inversen
einen stetigen Inversen
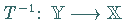 ,
wenn
,
wenn 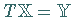 und mit einer Konstanten
und mit einer Konstanten
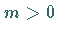 für alle
für alle 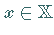 die Abschätzung
die Abschätzung 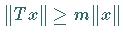 gilt.
Man hat dann sogar
gilt.
Man hat dann sogar
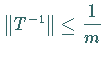 .
.
Im Falle von BANACH-Räumen 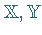 gilt der
Satz von BANACH.
gilt der
Satz von BANACH.
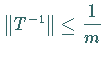 .
.