Der Satz von KREIN und LOSANOWSKIJ macht eine Aussage über die Stetigkeit
positiver linearer Operatoren.
Sind 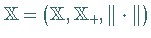 und
und 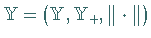 geordnete normierte
Räume, wobei
geordnete normierte
Räume, wobei 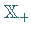 ein erzeugender Kegel ist, dann ist die Menge
ein erzeugender Kegel ist, dann ist die Menge 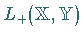 aller
positiven linearen und stetigen Operatoren
aller
positiven linearen und stetigen Operatoren 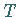 ,
d.h.
,
d.h. 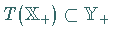 ,
ein
Kegel in
,
ein
Kegel in 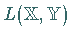 .
Dann besagt der Satz von M.G. KREIN, G.J. LOSANOWSKIJ (s. Lit. 12.20):
Sind
.
Dann besagt der Satz von M.G. KREIN, G.J. LOSANOWSKIJ (s. Lit. 12.20):
Sind  und
und 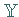 geordnete BANACH-Räume mit abgeschlossenen Kegeln
geordnete BANACH-Räume mit abgeschlossenen Kegeln 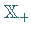 und
und
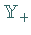 und erzeugendem
und erzeugendem 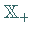 ,
dann folgt aus der Positivität eines linearen Operators
seine Stetigkeit.
,
dann folgt aus der Positivität eines linearen Operators
seine Stetigkeit.