Existenz einer Basis. Isomorphe Hilbert-Räume
In jedem separablen HILBERT-Raum existiert eine Basis.
Daraus ergibt sich, daß jedes orthonormale System zu einer Basis ergänzt
werden kann.
Zwei HILBERT-Räume 
und 
heißen
isomorph (oder isomorph als HILBERT-Räume) ,
wenn es eine lineare, bijektive Abbildung
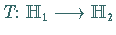mit der
Eigenschaft 
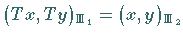(also eine das Skalarprodukt und wegen
(12.106) auch die Norm erhaltende Abbildung) gibt.
Es gilt: Zwei beliebige unendlichdimensionale separable HILBERT-Räume sind
stets isometrisch, also insbesondere ist jeder solche Raum isometrisch
zu dem separablen Raum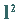 
.
