Seien jetzt 
ein separabler HILBERT-Raum und
 |
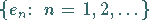(12.122) |
ein fixiertes orthonormales System in 
.
Für ein Element 
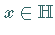heißen die Zahlen 
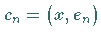FOURIER-Koeffizienten des Elements 
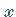bezüglich des Systems
(12.122).
Die (formale) Reihe
 |
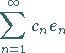(12.123) |
nennt man FOURIER-Reihe des Elements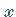
bezüglich des Systems
(12.122).
Die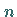 
-te Partialsumme der FOURIER-Reihe eines Elements
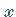besitzt die
Eigenschaft der Bestapproximation , d.h., bei festem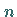
ergibt unter allen Vektoren
aus 
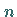die -te Partialsumme der FOURIER-Reihe,
also das Element
 |
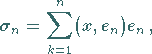(12.124) |
den kleinsten Wert für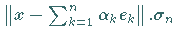 
ist orthogonal zu 
,
und es gilt die BESSELsche Ungleichung
 |
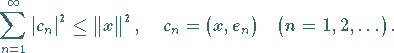(12.125) |
