Sobolew-Räume
Sei 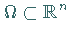 ein beschränktes Gebiet (d.h. eine offene zusammenhängende
Menge) mit hinreichend glattem Rand
ein beschränktes Gebiet (d.h. eine offene zusammenhängende
Menge) mit hinreichend glattem Rand 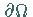 .
Für
.
Für  oder
oder 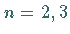 stelle man sich
stelle man sich 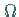 etwa als ein Intervall
etwa als ein Intervall 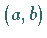 oder
eine konvexe Menge vor.
Eine Funktion
oder
eine konvexe Menge vor.
Eine Funktion 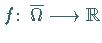 nennt man
nennt man 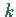 -mal
stetig differenzierbar in dem abgeschlossenen Gebiet
-mal
stetig differenzierbar in dem abgeschlossenen Gebiet  ,
wenn
,
wenn
a)  auf
auf 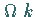 -mal stetig differenzierbar ist und
-mal stetig differenzierbar ist und
b) jede ihrer partiellen Ableitungen einen Grenzwert besitzt, wenn 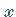 zu einem
beliebigen Randpunkt von
zu einem
beliebigen Randpunkt von 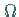 konvergiert;
konvergiert;
mit anderen Worten, jede partielle Ableitung von  ist stetig auf den Rand von
ist stetig auf den Rand von 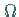 fortsetzbar.
fortsetzbar.
In diesem Vektorraum wird mit dem LEBESGUE-Maß 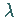 im
im
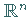 die folgende Norm eingeführt:
die folgende Norm eingeführt:
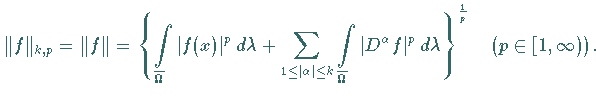 |
|
|
(12.88) |
Der entstandene normierte Raum wird mit 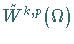 bezeichnet
(im Unterschied zu dem mit einer ganz anderen Norm versehenen Raum
bezeichnet
(im Unterschied zu dem mit einer ganz anderen Norm versehenen Raum
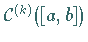 ).
Hier bedeutet
).
Hier bedeutet 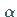 einen Multiindex , d.h. ein geordnetes
einen Multiindex , d.h. ein geordnetes 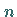 -Tupel
-Tupel
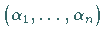 von nichtnegativen ganzen Zahlen, wobei die Summe der
Komponenten von
von nichtnegativen ganzen Zahlen, wobei die Summe der
Komponenten von 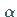 mit
mit 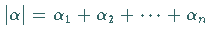 bezeichnet wird.
Für eine Funktion
bezeichnet wird.
Für eine Funktion 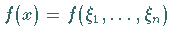 mit
mit
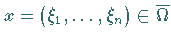 nutzt man - wie in (12.88) -
die verkürzte Schreibweise
nutzt man - wie in (12.88) -
die verkürzte Schreibweise
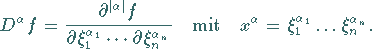 |
(12.89) |
Der normierte Raum 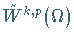 ist nicht vollständig.
Seine Vervollständigung wird mit
ist nicht vollständig.
Seine Vervollständigung wird mit 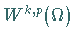 oder im Falle von
oder im Falle von 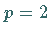 mit
mit
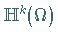 bezeichnet und heißt SOBOLEW-Raum .
bezeichnet und heißt SOBOLEW-Raum .
![]() ist nicht vollständig.
Seine Vervollständigung wird mit
ist nicht vollständig.
Seine Vervollständigung wird mit ![]() oder im Falle von
oder im Falle von ![]() mit
mit
![]() bezeichnet und heißt SOBOLEW-Raum .
bezeichnet und heißt SOBOLEW-Raum .