Jede Teilmenge 
eines metrischen Raumes 
liegt in der abgeschlossenen Menge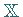 
.
Es existiert immer eine kleinste abgeschlossene Menge, die
enthält, nämlich der
Durchschnitt aller abgeschlossenen Mengen aus ,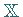
die
enthalten.
Diese Menge heißt abgeschlossene Hülle oder Abschließung der Menge
und wird gewöhnlich mit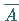 
bezeichnet.
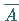ist mit der Menge aller Berührungspunkte von
identisch; man erhält
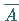aus der Menge
durch Hinzufügen aller ihrer Häufungspunkte.
Abgeschlossene Mengen sind gerade solche Mengen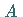 
,
für die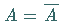 
gilt.
Demzufolge erlauben sie eine Charakterisierung durch Folgen in folgender Weise:
ist abgeschlossen genau dann, wenn für eine beliebige Folge
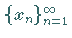von Elementen aus
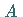die im Raum
zu einem Element
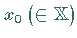konvergiert, der Grenzwert 
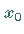zu
gehört.
