Abgeschlossene Mengen
Eine Teilmenge 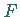 eines metrischen Raumes
eines metrischen Raumes  heißt abgeschlossen , wenn
heißt abgeschlossen , wenn
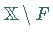 eine offene Menge ist.
Jede abgeschlossene Kugel in einem metrischen Raum, insbesondere jedes Intervall der Typen
eine offene Menge ist.
Jede abgeschlossene Kugel in einem metrischen Raum, insbesondere jedes Intervall der Typen
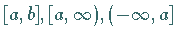 in
in 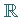 ,
ist eine abgeschlossene Menge.
,
ist eine abgeschlossene Menge.
Dual zu den Axiomen der offenen Mengen erfüllt die Gesamtheit aller abgeschlossenen
Mengen eines metrischen Raumes folgende Eigenschaften:
- Sind
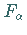 für
für 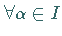 abgeschlossen, dann ist
auch die Menge
abgeschlossen, dann ist
auch die Menge 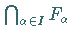 abgeschlossen.
abgeschlossen.
- Sind
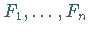 beliebig endlich viele abgeschlossene Mengen, dann ist auch
die Menge
beliebig endlich viele abgeschlossene Mengen, dann ist auch
die Menge 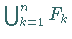 abgeschlossen.
abgeschlossen.
- Die leere Menge
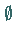 ist vereinbarungsgemäß abgeschlossen.
ist vereinbarungsgemäß abgeschlossen.
Die Mengen 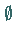 und
und 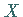 sind sowohl offen als auch abgeschlossen.
Ein Punkt
sind sowohl offen als auch abgeschlossen.
Ein Punkt 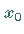 des metrischen Raumes
des metrischen Raumes  heißt Berührungspunkt der
Menge
heißt Berührungspunkt der
Menge 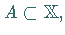 wenn für jede Umgebung
wenn für jede Umgebung 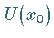
 |
(12.53) |
gilt.
Besteht dieser Durchschnitt darüber hinaus jeweils nicht nur aus dem einen Punkt
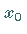 ,
dann heißt
,
dann heißt 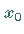 Häufungspunkt der Menge
Häufungspunkt der Menge  .
Ein Berührungspunkt, der kein Häufungspunkt ist, heißt isolierter
Punkt.
.
Ein Berührungspunkt, der kein Häufungspunkt ist, heißt isolierter
Punkt.
Ein Häufungspunkt von  muß somit nicht unbedingt zur Menge
muß somit nicht unbedingt zur Menge  gehören muß, z.B. der Punkt
gehören muß, z.B. der Punkt 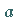 im Verhältnis zur Menge
im Verhältnis zur Menge 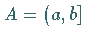 ,
während ein isolierter Punkt notwendigerweise zur Menge
,
während ein isolierter Punkt notwendigerweise zur Menge  gehören muß.
Ein Punkt
gehören muß.
Ein Punkt 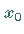 ist genau dann Berührungspunkt der Menge
ist genau dann Berührungspunkt der Menge 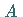 ,
wenn es eine Folge
,
wenn es eine Folge
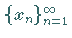 von Elementen
von Elementen 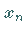 aus
aus  gibt, die zu
gibt, die zu 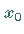 konvergiert, wobei
konvergiert, wobei
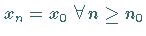 im Falle eines isolierten Punktes
im Falle eines isolierten Punktes 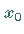 gesetzt wird.
gesetzt wird.
![]() und
und ![]() sind sowohl offen als auch abgeschlossen.
Ein Punkt
sind sowohl offen als auch abgeschlossen.
Ein Punkt ![]() des metrischen Raumes
des metrischen Raumes ![]() heißt Berührungspunkt der
Menge
heißt Berührungspunkt der
Menge ![]() wenn für jede Umgebung
wenn für jede Umgebung ![]()
![]() muß somit nicht unbedingt zur Menge
muß somit nicht unbedingt zur Menge ![]() gehören muß, z.B. der Punkt
gehören muß, z.B. der Punkt ![]() im Verhältnis zur Menge
im Verhältnis zur Menge ![]() ,
während ein isolierter Punkt notwendigerweise zur Menge
,
während ein isolierter Punkt notwendigerweise zur Menge ![]() gehören muß.
Ein Punkt
gehören muß.
Ein Punkt ![]() ist genau dann Berührungspunkt der Menge
ist genau dann Berührungspunkt der Menge ![]() ,
wenn es eine Folge
,
wenn es eine Folge
![]() von Elementen
von Elementen ![]() aus
aus ![]() gibt, die zu
gibt, die zu ![]() konvergiert, wobei
konvergiert, wobei
![]() im Falle eines isolierten Punktes
im Falle eines isolierten Punktes ![]() gesetzt wird.
gesetzt wird.