Seien 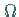 eine kompakte Teilmenge aus
eine kompakte Teilmenge aus 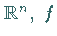 eine den
CARATHEODORY-Bedingungen genügende und
eine den
CARATHEODORY-Bedingungen genügende und 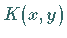 eine stetige Funktion
auf
eine stetige Funktion
auf 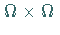 .
Der nichtlineare Operator
.
Der nichtlineare Operator 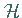 auf
auf 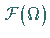
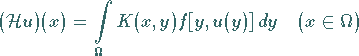 |
(12.188) |
heißt HAMMERSTEIN-Operator .
Mit dem linearen von 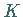 als Kern erzeugten Integraloperator
als Kern erzeugten Integraloperator 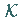
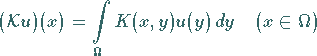 |
(12.189) |
kann 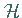 in der Form
in der Form 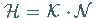 geschrieben werden.
Genügt nun der Kern
geschrieben werden.
Genügt nun der Kern 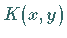 der Bedingung
der Bedingung
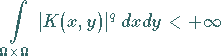 |
(12.190) |
und die Funktion  der Bedingung (12.187), dann ist
der Bedingung (12.187), dann ist 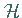 ein stetiger und
kompakter Operator auf
ein stetiger und
kompakter Operator auf 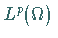 .
.