Adjungierter Operator zu einem unbeschränkten Operator
Seien 
und 
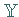reelle normierte Räume und 
ein linearer (nicht unbedingt
beschränkter) Operator mit dem (linearen) Definitionsbereich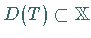 
und
Werten in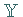 
.
Für ein fixiertes Funktional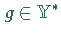 
ist dann der Ausdruck 
,
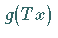der
offenbar linear von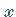 
abhängt, sinnvoll, so daß die Frage nach der Existenz
eines wohlbestimmten Funktionals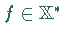 
mit der Eigenschaft
 |
(12.178) |
steht.
Sei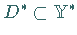 
die Menge aller der 
,
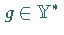für die bei einem gewissen
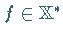die Darstellung (12.178) gilt.
Ist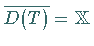 
,
dann ist 
zu vorgegebenem 
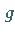eindeutig bestimmt, so
daß ein linearer Operator 
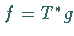mit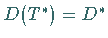 
als Definitionsbereich entsteht.
Für beliebige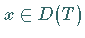 
und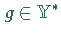
gilt dann
 |
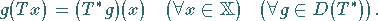(12.179) |
Der Operator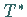 
ist sogar abgeschlossen und heißt adjungiert zu 
.
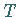Die Natürlichkeit dieses allgemeinen Zugangs ergibt sich daraus, daß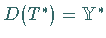 
genau dann gilt, wenn
auf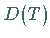 
beschränkt ist.
In diesem Falle ist 
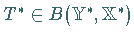und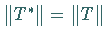 
.
