Bestimmung einer normierten Funktion 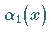 ,
die zu allen Funktionen aus
,
die zu allen Funktionen aus
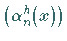 orthogonal ist.
Für
orthogonal ist.
Für 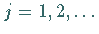 werden jeweils die folgenden Schritte durchlaufen:
werden jeweils die folgenden Schritte durchlaufen:
1. Berechnung der Funktion 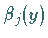 sowie einer Zahl
sowie einer Zahl 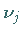 aus
aus
wobei 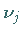 immer ungleich Null und so zu bestimmen ist, daß
immer ungleich Null und so zu bestimmen ist, daß 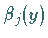 normiert
ist.
normiert
ist.
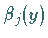 ist orthogonal zu allen Funktionen
ist orthogonal zu allen Funktionen
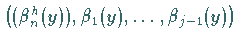 .
.
2. Bestimmung der Funktion 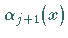 sowie einer Zahl
sowie einer Zahl 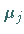 aus
aus
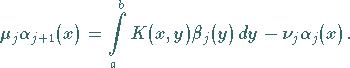 |
(11.52c) |
Es können zwei Fälle eintreten:
a) 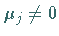 :
Die Funktion
:
Die Funktion 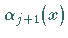 ist orthogonal zu allen
Funktionen
ist orthogonal zu allen
Funktionen 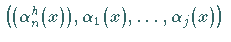 .
.
b) 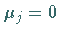 :
Die Funktion
:
Die Funktion 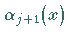 ist nicht eindeutig bestimmt.
Erneut werden zwei Fälle unterschieden:
ist nicht eindeutig bestimmt.
Erneut werden zwei Fälle unterschieden:
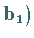 Das System
Das System
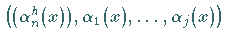 ist vollständig.
Dann ist auch das System
ist vollständig.
Dann ist auch das System
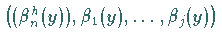 vollständig, und das
Verfahren ist beendet.
vollständig, und das
Verfahren ist beendet.
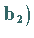 Das System
Das System
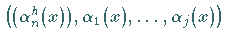 ist nicht vollständig.
Dann wird eine beliebige, zu diesen Funktionen orthogonale Funktion
ist nicht vollständig.
Dann wird eine beliebige, zu diesen Funktionen orthogonale Funktion 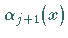 gewählt.
gewählt.
Das Verfahren wird so lange wiederholt, bis die Orthonormalsysteme vollständig sind.
Es ist möglich, daß im Algorithmus von einem gewissen Schritt ab auch nach
abzählbar unendlich vielen weiteren Schritten nicht der Fall b) eintritt.
Ist die dabei erzeugte abzählbar unendliche Folge von Funktionen
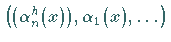 nicht vollständig, dann kann mit
einer zu allen diesen Funktionen orthogonalen Funktion
nicht vollständig, dann kann mit
einer zu allen diesen Funktionen orthogonalen Funktion 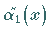 das
Verfahren neu gestartet werden.
das
Verfahren neu gestartet werden.
Werden die durch das Verfahren ermittelten Funktionen 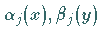 sowie die
Zahlen
sowie die
Zahlen 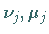 geeignet umbezeichnet, dann läßt sich die resultierende
Kernmatrix
geeignet umbezeichnet, dann läßt sich die resultierende
Kernmatrix 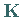 folgendermaßen darstellen:
folgendermaßen darstellen:
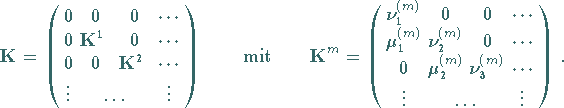 |
(11.53) |
Die Matrizen 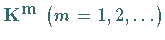 sind endlich, wenn im
Algorithmus nach endlich vielen Schritten der Fall
sind endlich, wenn im
Algorithmus nach endlich vielen Schritten der Fall 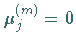 eintritt.
Dagegen sind sie unendlich, wenn für abzählbar unendlich viele Schritte
eintritt.
Dagegen sind sie unendlich, wenn für abzählbar unendlich viele Schritte 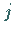 gilt:
gilt:
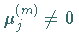 .
Die Anzahl der Nullzeilen bzw. Nullspalten in
.
Die Anzahl der Nullzeilen bzw. Nullspalten in 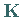 entspricht der Anzahl der
Funktionen in den Systemen
entspricht der Anzahl der
Funktionen in den Systemen 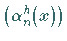 bzw.
bzw. 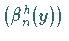 .
Ein besonders einfacher Fall liegt vor, wenn die Matrizen
.
Ein besonders einfacher Fall liegt vor, wenn die Matrizen 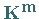 nur eine
Zahl
nur eine
Zahl 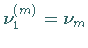 enthalten, also alle Zahlen
enthalten, also alle Zahlen 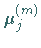 gleich Null sind.
gleich Null sind.
Mit den Bezeichnungen aus dem Abschnitt Zurückführung der
Integralgleichung auf ein lineares Gleichungssystem ergibt sich für die Lösung des
unendlichen Gleichungssystems unter der Voraussetzung von 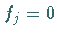 für
für
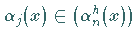 :
:
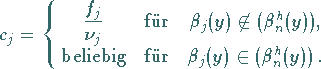 |
(11.54) |
![]() sowie die
Zahlen
sowie die
Zahlen ![]() geeignet umbezeichnet, dann läßt sich die resultierende
Kernmatrix
geeignet umbezeichnet, dann läßt sich die resultierende
Kernmatrix ![]() folgendermaßen darstellen:
folgendermaßen darstellen:
![]() für
für
![]() :
: