Im allgemeinen ist die Auflösung des unter Zurückführung
der Integralgleichung auf ein lineares Gleichungssystem aufgestellten unendlichen linearen
Gleichungssystems nicht einfacher als die Lösung des Ausgangsproblems.
Durch geeignete Wahl der Orthonormalsysteme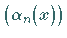 
und 
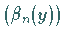kann jedoch
die Struktur der Kernmatrix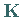 
so beeinflußt werden, daß sich das
Gleichungssystem einfach lösen läßt.
Das folgende Verfahren konstruiert zwei Orthonormalsysteme, die eine Kernmatrix liefern,
deren Koeffizienten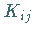 
nur für 
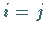und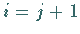 
ungleich Null sind.
Mit der Methode des voranstehenden Abschnittes werden zunächst zwei orthonormierte
Lösungssysteme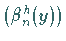 
bzw.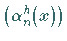 
der homogenen Integralgleichung
bzw. der dazu transponierten homogenen Gleichung bestimmt, d.h., alle Lösungen dieser
zwei Integralgleichungen lassen sich durch Linearkombination der Funktionen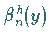 
bzw.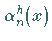 
darstellen.
Diese Orthonormalsysteme sind nicht vollständig.
Mit dem folgenden Verfahren werden diese Systeme durch schrittweises Hinzufügen von
Funktionen 
,
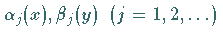zu vollständigen
Orthonormalsystemen ergänzt.
