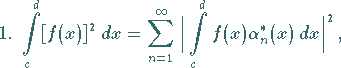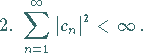Zur Lösung der Integralgleichung
 |
(11.55a) |
bildet man mit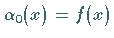 
für 
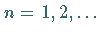die Funktionen
 |
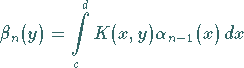(11.55b) |
und
 |
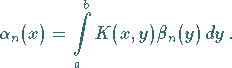(11.55c) |
Existiert eine quadratisch integrierbare Lösung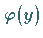 
von
(11.55a), dann gilt:
Durch Orthogonalisierung und Normierung der nach (11.55b,c) ermittelten
Funktionensysteme erhält man die Orthonormalsysteme
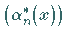und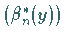 
.
Wird hierzu das SCHMIDTsche Orthogonalisierungsverfahren verwendet, dann besitzt
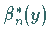die Darstellung
 |
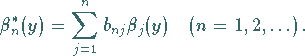(11.55e) |
Es wird nun angenommen, daß die Lös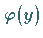ung
der Gleichung (11.55a)
die Reihendarstellung
 |
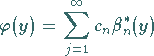(11.55f) |
besitzt.
In diesem Fall gilt für die Koeffizienten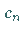 
unter Beachtung von (11.55d)
 |
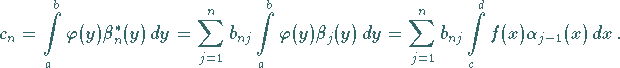(11.55g) |
Für die Existenz einer Lösungsdarstellung (11.55f) sind die folgenden
Bedingungen notwendig und hinreichend:
 |
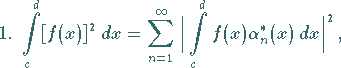(11.56a) |
 |
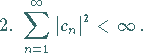(11.56b) |
