Erste und zweite Variation
Bei der Herleitung der EULERschen Differentialgleichung mit Hilfe von
Vergleichsfunktionen wurde die TAYLOR-Entwicklung des
Integranden von
 |
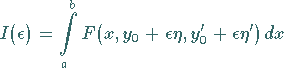(10.62) |
nach den bezüglich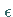 
linearen Gliedern abgebrochen.
Berücksichtigt man auch die quadratischen Glieder, dann erhält man
Bezeichnet man als
1. Variation
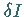des Funktionals 
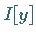den Ausdruck
 |
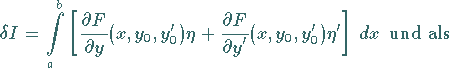(10.64) |
2. Variation
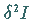des Funktionals
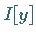den Ausdruck
 |
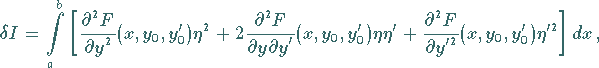(10.65) |
dann kann man schreiben:
 |
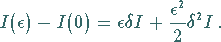(10.66) |
Mit Hilfe dieser Variationen lassen sich die verschiedenen Optimalitätsbedingungen für
das Funktional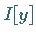
formulieren (s. Lit. 10.6).
