Mittelwerte
Mittelwerte zweidimensionaler Zufallsgrößen und
gewichtete Mittelwerte werden hier nicht betrachtet.
1. Arithmetisches Mittel
von 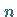 Größen
Größen 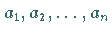 heißt
der Ausdruck
heißt
der Ausdruck
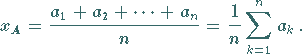 |
(1.68a) |
Für zwei Größen 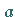 und
und 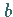 ergibt sich:
ergibt sich:
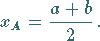 |
(1.68b) |
Die Größen 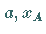 und
und 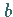 bilden eine arithmetische Folge.
bilden eine arithmetische Folge.
2. Geometrisches Mittel
von 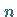 positiven Größen
positiven Größen 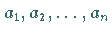 heißt der Ausdruck
heißt der Ausdruck
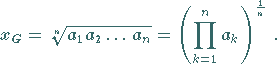 |
(1.69a) |
Für zwei Größen 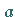 und
und 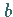 ergibt sich
ergibt sich
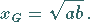 |
(1.69b) |
Die Größen 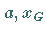 und
und 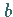 bilden eine geometrische Folge.
Wenn
bilden eine geometrische Folge.
Wenn 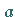 und
und 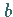 gegebene Strecken sind, dann kann eine Strecke der Länge
gegebene Strecken sind, dann kann eine Strecke der Länge
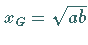 mit Hilfe einer der in den folgenden zwei Abbildungen angegebenen
Konstruktionen ermittelt werden.
mit Hilfe einer der in den folgenden zwei Abbildungen angegebenen
Konstruktionen ermittelt werden.
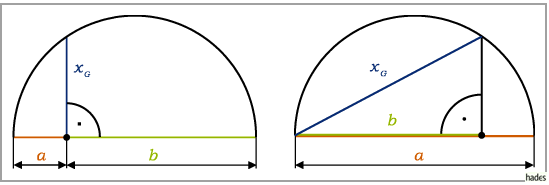
Einen speziellen Fall des geometrischen Mittels stellt die Teilung einer Strecke
im Verhältnis des Goldenen Schnittes dar.
3. Harmonisches Mittel
von 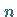 Größen
Größen 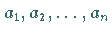 heißt
der Ausdruck
heißt
der Ausdruck
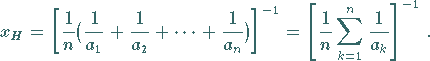 |
(1.70a) |
Für zwei Größen 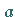 und
und 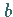 ergibt sich
ergibt sich
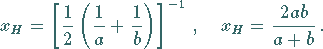 |
(1.70b) |
4. Quadratisches Mittel
von 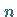 Größen
Größen 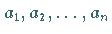 heißt
der Ausdruck
heißt
der Ausdruck
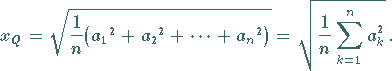 |
(1.71a) |
Für zwei Größen 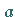 und
und 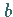 ergibt sich
ergibt sich
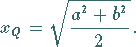 |
(1.71b) |
Das quadratische Mittel ist von Bedeutung für die Theorie der
Beobachtungsfehler.
5. Vergleich der Mittelwerte für zwei positive Größen a und b
Für 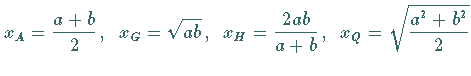 gilt
gilt
1. wenn
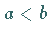
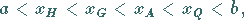 |
(1.72a) |
2. wenn
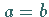
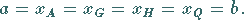 |
(1.72b) |
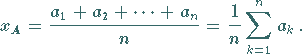
![]() und
und ![]() ergibt sich:
ergibt sich:
![]() und
und ![]() bilden eine arithmetische Folge.
bilden eine arithmetische Folge.
![]() positiven Größen
positiven Größen ![]() heißt der Ausdruck
heißt der Ausdruck
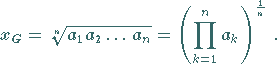
![]() und
und ![]() ergibt sich
ergibt sich
![]() und
und ![]() bilden eine geometrische Folge.
Wenn
bilden eine geometrische Folge.
Wenn ![]() und
und ![]() gegebene Strecken sind, dann kann eine Strecke der Länge
gegebene Strecken sind, dann kann eine Strecke der Länge
![]() mit Hilfe einer der in den folgenden zwei Abbildungen angegebenen
Konstruktionen ermittelt werden.
mit Hilfe einer der in den folgenden zwei Abbildungen angegebenen
Konstruktionen ermittelt werden.
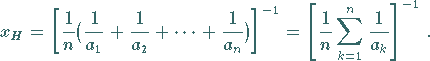
![]() und
und ![]() ergibt sich
ergibt sich
![]() Größen
Größen ![]() heißt
der Ausdruck
heißt
der Ausdruck
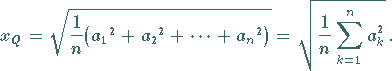
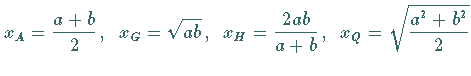 gilt
gilt