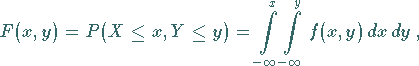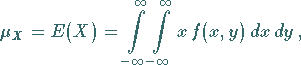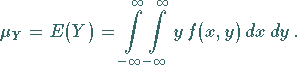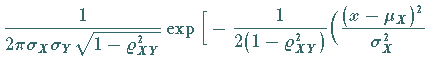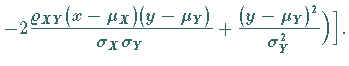Zwei Merkmale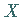 
und 
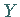sollen zu einer zweidimensionalen Zufallsgröße (
)
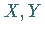mit folgenden Verteilungsfunktionen zusammengefaßt werden:
 |
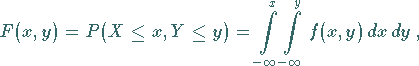(16.148a) |
 |
(16.148b) |
Die Zufallsgrößen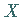
und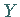
heißen unabhängig voneinander , wenn
 |
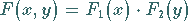(16.149) |
gilt.
Die wichtigsten Parameter einer zweidimensionalen Verteilung sind:
1. Mittelwerte:
 |
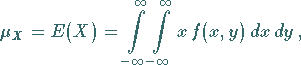(16.150a) |
 |
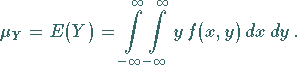(16.150b) |
2. Streuungen:
 |
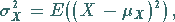(16.151a) |
 |
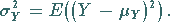(16.151b) |
3. Kovarianz:
 |
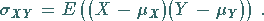(16.152) |
4. Korrelationskoeffizient:
 |
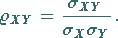(16.153) |
Der Korrelationskoeffizient ist ein Maß für die lineare Abhängigkeit von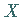
und
,
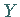denn es gilt:
Alle Punkte ()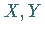
liegen genau dann mit der Wahrscheinlichkeit 1 auf einer Geraden, wenn
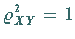ist.
Wenn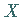
und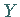
unabhängige Zufallsveränderliche sind, dann ist 
.
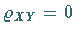Aus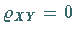 
kann man nur dann auf die Unabhängigkeit der Merkmale
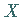und
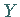schließen, wenn diese einer zweidimensionalen Normalverteilung genügen,
die durch die folgende Dichtefunktion definiert ist:
